はじめに
プロセスプラズマのシミュレーションツールとして、M. J. Kushner 教授により開発された HPEM (Hybrid Plasma Equipment Model) はあまりにも有名であり、これまでにHPEMを用いた数多くの研究成果が論文として発表されています。もともと HPEM は大学で開発されたものであり、使用に関しては計算設定のための膨大な数のパラメーターの意味を理解する必要があるため、一般企業などで使いこなすことは至難の業でした。英国の Quantemol 社は、容易にプラズマシミュレーションが実行できるように、HPEM のフロントエンドとなる グラフィカル ユーザー インターフェイス (GUI) を開発し、 HPEM と組み合わせて Q-VT (Quantemol-Virtual Tool) としてライセンス販売しています。
前回の記事では同一電極にRF 2 周波重畳したパルス変調 CCP のシミュレーション例を紹介しました。今回も類似した方式の CCP ですが、高周波側 RF は連続波(CW)で、低周波側 RF のみパルス変調する方式の CCP の計算を試みましたので簡単に紹介します。この CCP は言い換えれば、2周波重畳駆動と単周波駆動を交互に切り替えている方式になります。今回はウェハに入射するイオンのエネルギー及び角度分布(IEAD: Ion Energy and Angular Distributions)も算出しています。なお今回計算したモデルは実際に存在するプロセスを模したものではなく、あくまでも Q-VT の機能紹介の目的で想定した仮想モデルです。
装置モデル・計算条件
装置形状モデル・計算用グリッドを Fig. 1 に示します。これは前回のモデルと同じものです。グリッド数は 43 X 33 と非常に粗くなっていますが、本稿の目的が Q-VT の機能の紹介であるため計算精度は犠牲にし、計算スピードを優先しました。今回のプロセス条件も前回のモデルと全く同じですが、RF 駆動方式が異なっています。駆動電極には、ブロッキング コンデンサを介して 40 MHz, 100 W と 2 MHz, 20 W の RF 電力が重畳され供給されますが、40 MHz の電力は連続波(CW)として、また 2 MHz の電力は周波数 10 kHz でパルス変調されて供給されます。Duty 比は 50% と 25% の設定で計算結果を比較しました。
重粒子に対するタイムステップは 500 ns としました。また batres (コマンドライン上のスクリプト: 当社独自のもので Quantemol 社とは無関係)を用いて条件を変更したリスタート計算を交互に繰り返すことにより、最初から 7 パルスまで(累計 1400 iteration)の CCP の時間発展を計算しています。これに要したCPU時間は、前回と同様の環境で約 4 時間でした。
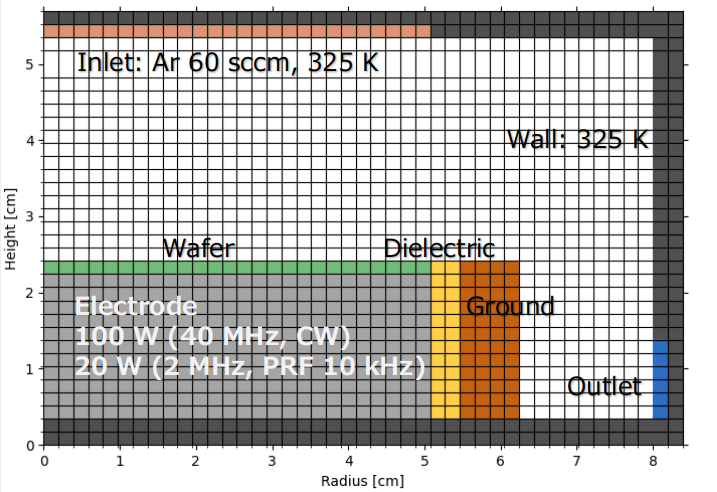
Fig. 1 装置形状モデル・計算用グリッド (グリッド数 43 X 33)
反応モデル
前回と同じ Ar ガスの反応モデルを用いているのでここでは省略します。
プラズマの時間発展(Duty 比 50%)
パルス Duty 比 50% の場合の、第 7 パルスまでの、平均電子密度、DCバイアス、トータルパワー、2つのRF周波数電圧の時間発展の様子を Fig. 2(a) に示します。また Fig. 2(b) に平均電子密度とプラズマ電位の時間発展を示します。プラズマ電位は実際には RF 振動しているため Fig. 2(b) 上では塗りつぶされたようなグラフになっています。パルスの ON/OFF に伴い、プラズマが変化する様子が明瞭に再現されています。また 7 パルスではまだ収束(周期定常状態)には至っていませんが、それでもかなり周期定常に近い状態まで達していることが伺えます。特徴的なことは、2 MHz-RF 電力の ON-Pulse 位相時は、OFF-Pulse 位相時よりも電子密度が減少することです。ON-Pulse 位相時は、負のバイアス電圧、プラズマ電位が増加してイオンの引き込みが増すため、電子密度が減少するものと考えられます(本稿では示しませんが実際に電極へのイオンフラックスが ON-Pulse 位相時に増すという結果が得られています)。同時にプラズマ電位とバイアス電圧の差により決定される入射イオンエネルギーも増加することが予想されますが、これは後に示す IEAD の計算により確認されます。
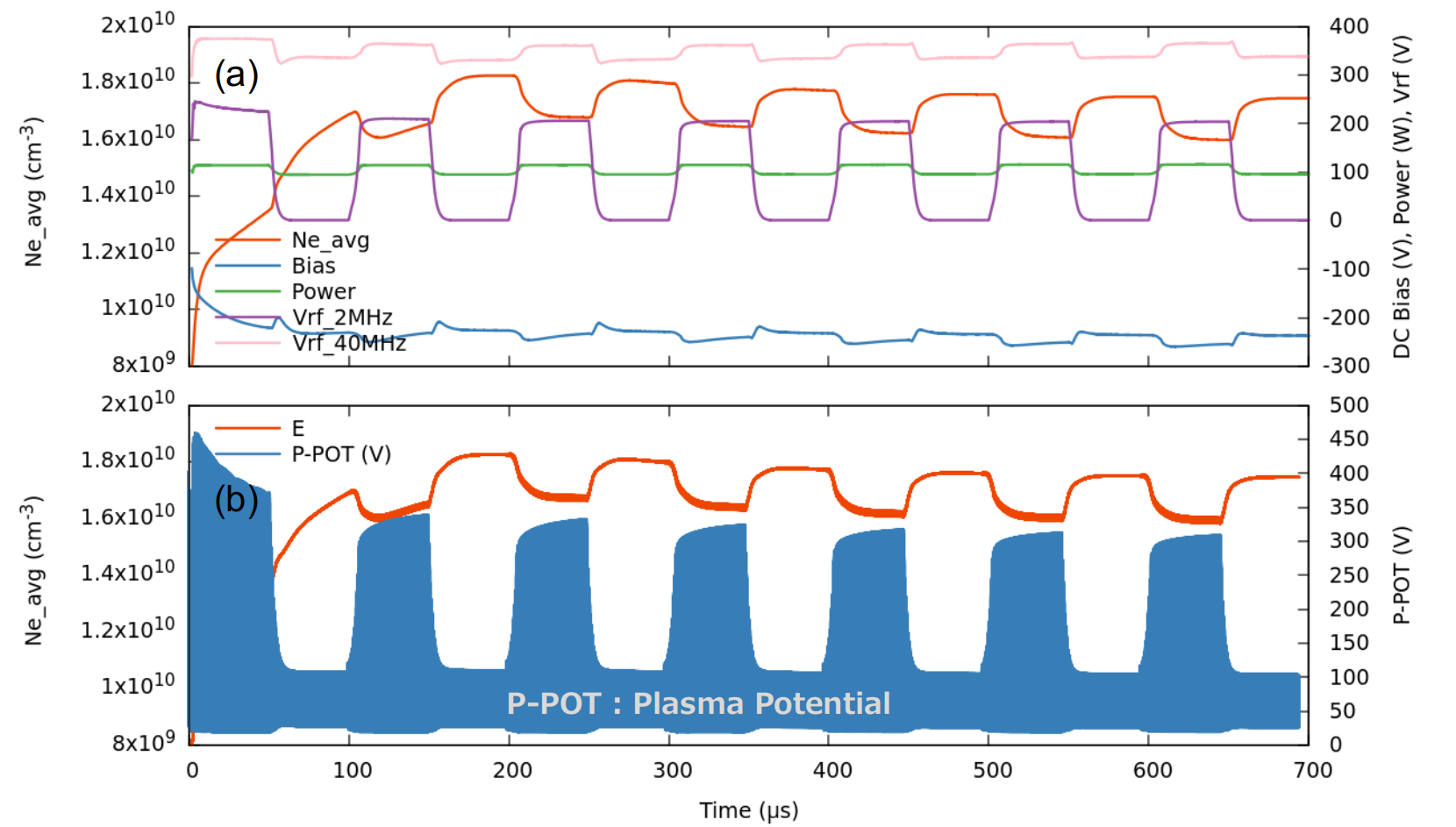
Fig. 2 パルス Duty 比 50% の場合の、平均電子密度、DC バイアス、トータルパワー、2つの RF 周波数電圧 (a)
及び 平均電子密度、プラズマ電位 (b) の時間発展の様子
Fig. 3 にパルス Duty 比 50% の場合の、第 7 パルス時の様子を拡大表示しました。今回の計算例ではパルス電圧の立ち上がり時間はおよそ 7 μs 程度でした。
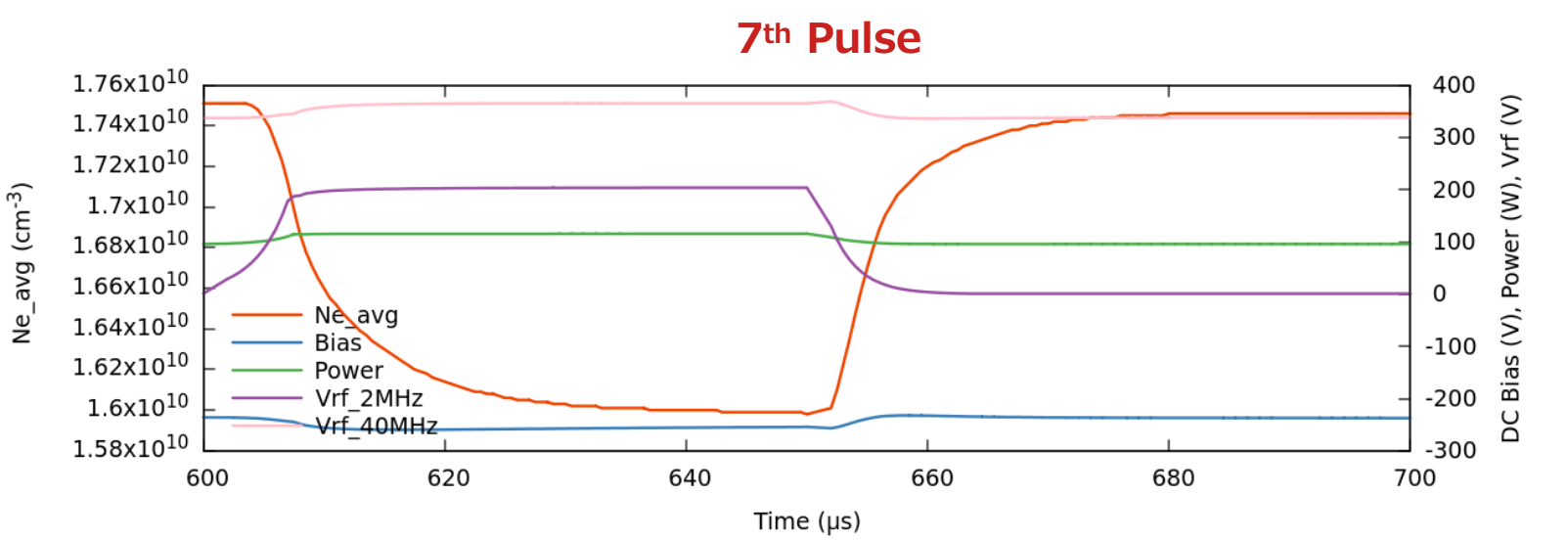
Fig. 3 パルス Duty 比 50% の場合の、第 7 パルス時の平均電子密度、DCバイアス、トータルパワー、
2 つの RF 周波数電圧の時間変化
プラズマ分布の時間変化(Duty 比 50%)
Fig. 4 は、パルス Duty 比 50% の場合の、電子密度分布、電子温度分布、イオン速度分布、平均電位分布の、第 7 パルス時における時間変化のアニメーションです。本パルス変調 CCP の特徴を具体的・視覚的に理解するのに役立つものと思われます。
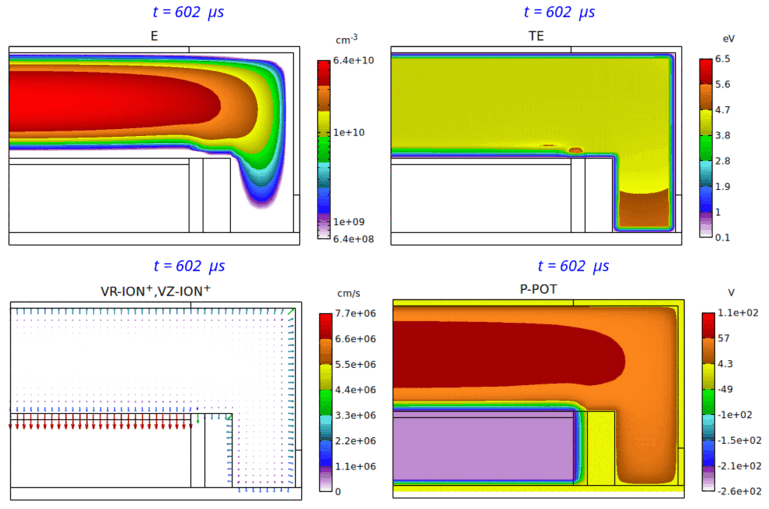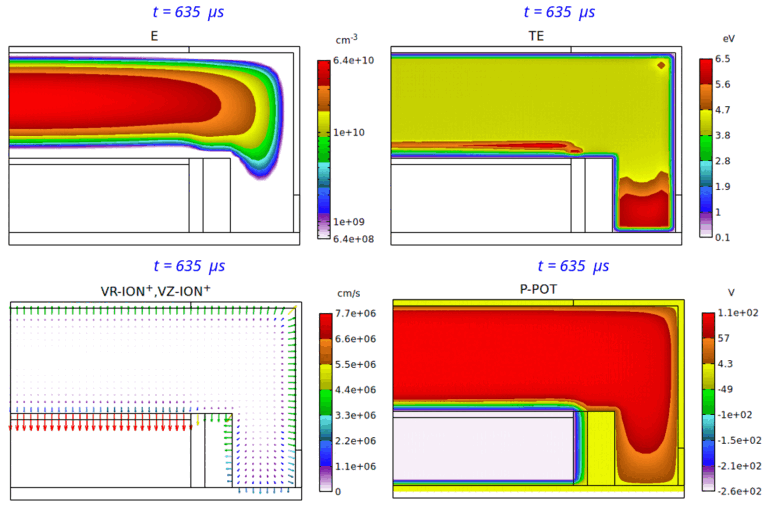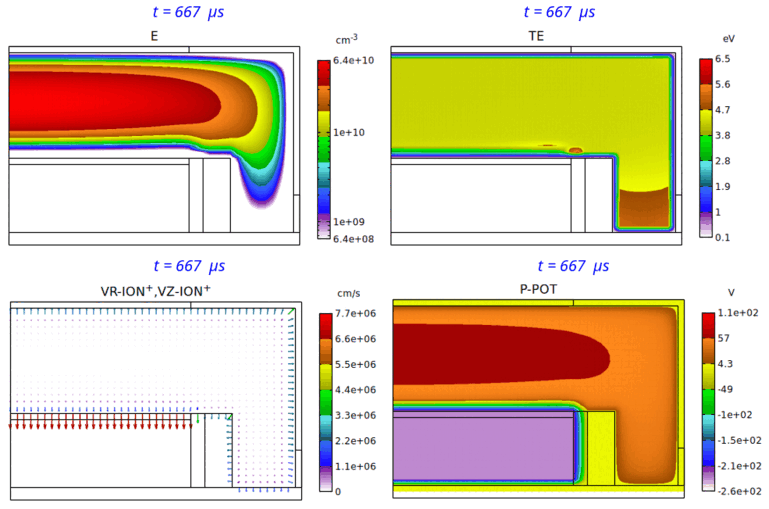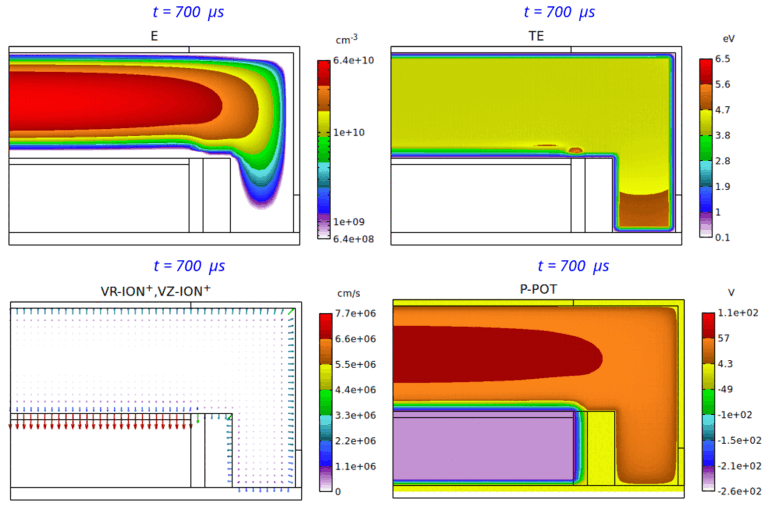
Fig. 4 パルス Duty 比 50% の場合の、電子密度 (E) 分布 ( 2-decade の対数スケール表示)、電子温度 (TE) 分布、
イオン速度 (VR-ION+,VZ-ION+) 分布、平均電位 (P-POT) 分布の時間変化
IEAD(Duty 比 50%)
HPEM 内臓の PCMC (Plasma Chemistry Monte Carlo) モジュールを用いて、ウェハ入射イオンのエネルギー・角度分布 IEAD を計算しました。Fig. 5(a), (b) に ON-Pulse/OFF-Pulse 終了直前の瞬時 IEAD を、Fig. 5(c), (d) にON-Pulse/OFF-Pulse の位相平均 IEAD を示します。Fig. 5(a), (b) を見ると、OFF-Pulse 位相時、すなわち 40 MHz だけで維持されている CCP では、エネルギーに対し単峰型の分布を示しているのに対し、低周波 2 MHz が加わる ON-Pulse 時には、典型的な双峰型の分布が高エネルギー側に重なって出現しています。プラズマのテキストにあるように、単峰型の分布はイオンが RF 電界に追従できないこと、双峰型の分布はイオンが RF 電界にある程度追従できること、に対応したものです。このように基本となる単峰型の IEAD の上に双峰型 IEAD が重なった、云わば "二階建て構造" の双峰型 IEAD が 2 周波重畳 CCP の特徴と考えられます。なお、Fig. 5(d) に見られる高エネルギー側のテールは、バルス電圧の立ち下がり遷移中の入射イオンの影響を受けたものと考えられます。
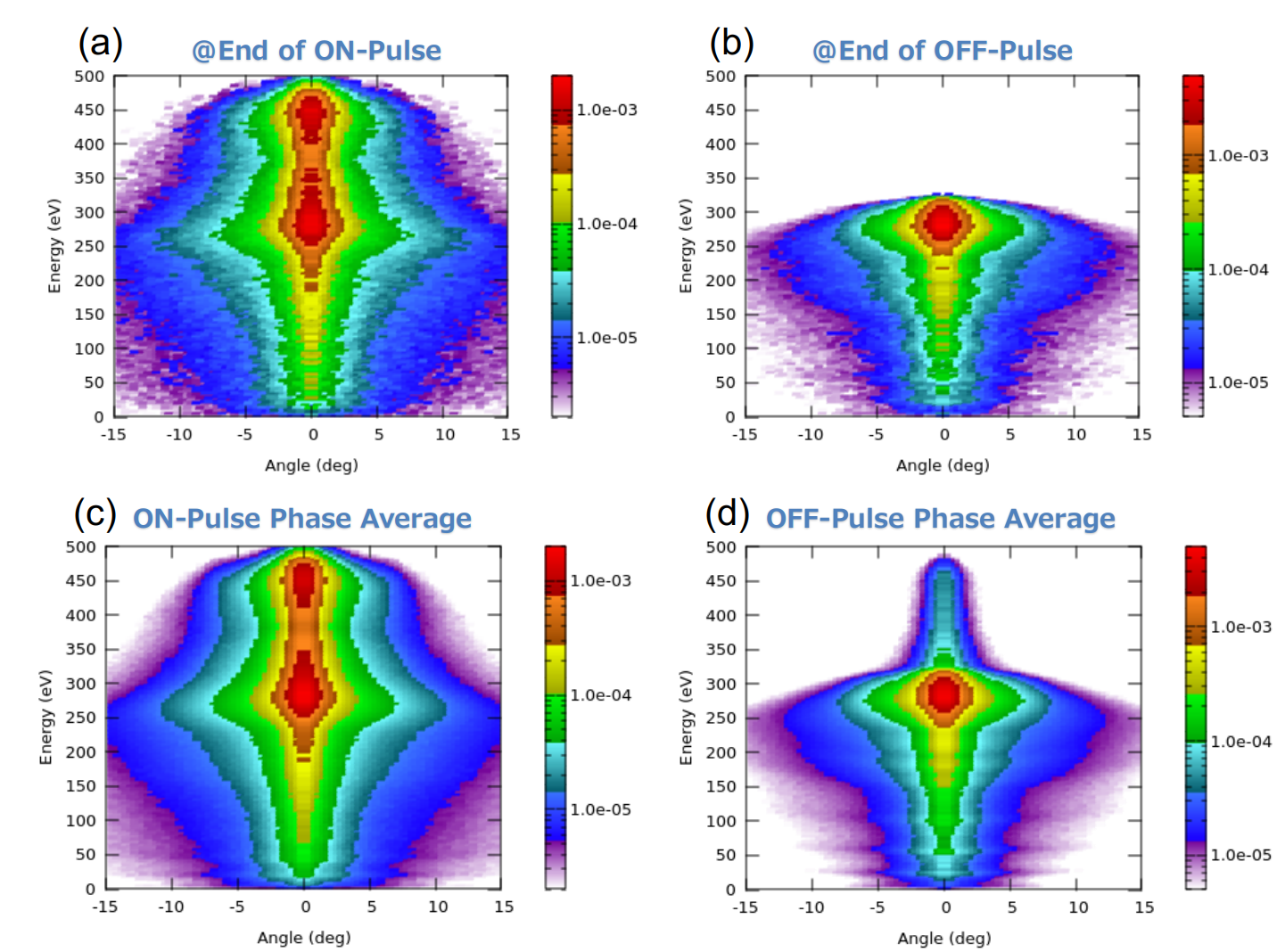
Fig. 5 パルス Duty 比 50% の場合の IEADs ( 3-decade の対数スケール表示) : ON-Pulse 終了直前の瞬時 IEAD (a)、
OFF-Pulse 終了直前の瞬時 IEAD (b)、ON-Pulse 位相平均 IEAD (c)、OFF-Pulse 位相平均 IEAD (d)
プラズマの時間発展(Duty 比 25%)
パルス Duty 比 25% の場合の、第 7 パルスまでの、平均電子密度、DCバイアス、トータルパワー、2つのRF周波数電圧の時間発展の様子を Fig. 6(a) に示します。また Fig. 6(b) に平均電子密度とプラズマ電位の時間発展を示します。
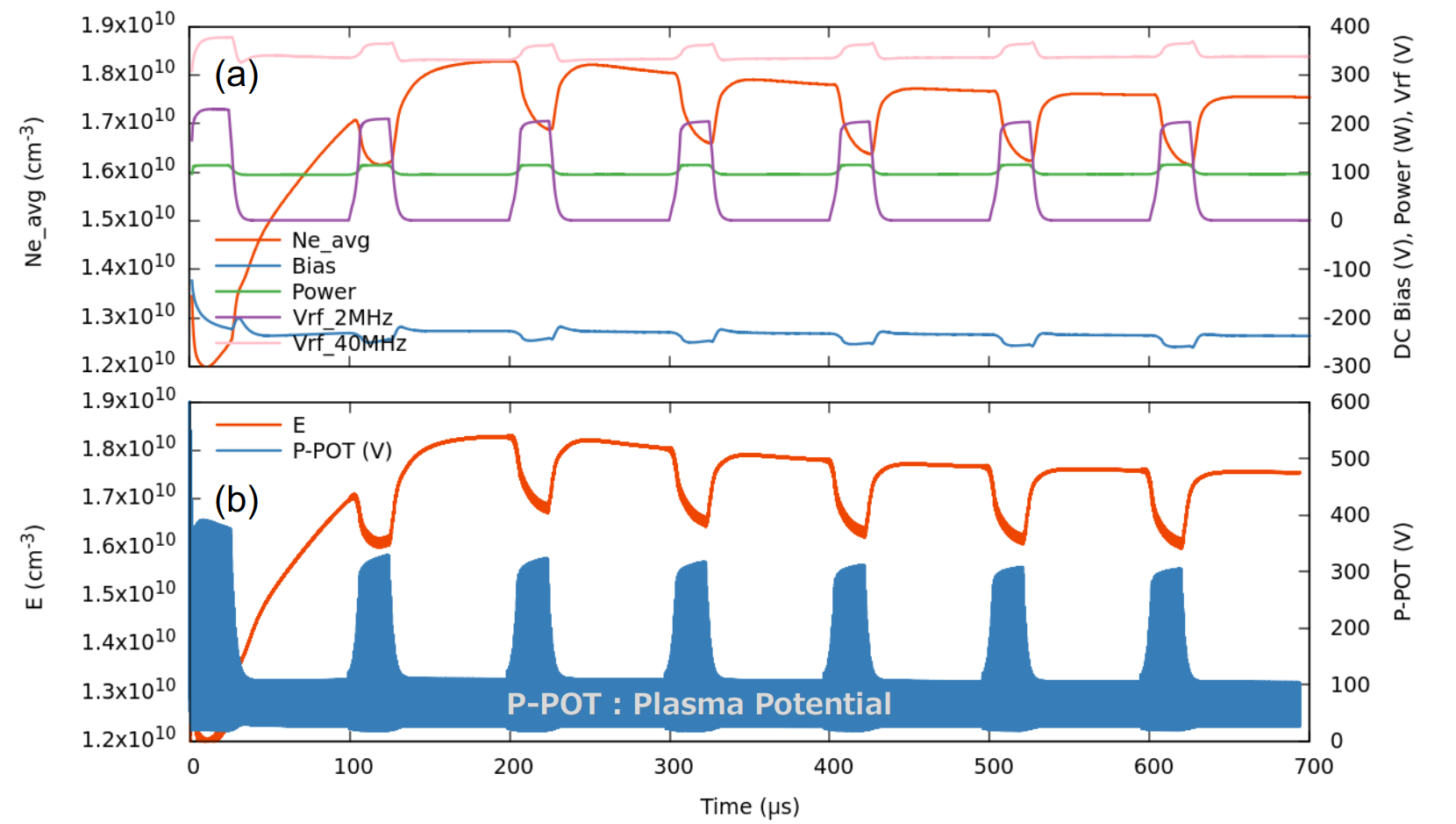
Fig. 6 パルス Duty 比 25% の場合の、平均電子密度、DC バイアス、トータルパワー、2つの RF 周波数電圧 (a)
及び 平均電子密度、プラズマ電位 (b) の時間発展の様子
Fig. 7 にパルス Duty 比 25% の場合の、第 7 パルス時の様子を拡大表示しました。パルス電圧の立ち上がり・立ち下がりの変化は Duty 比 50% の場合と同様なものとなっています。
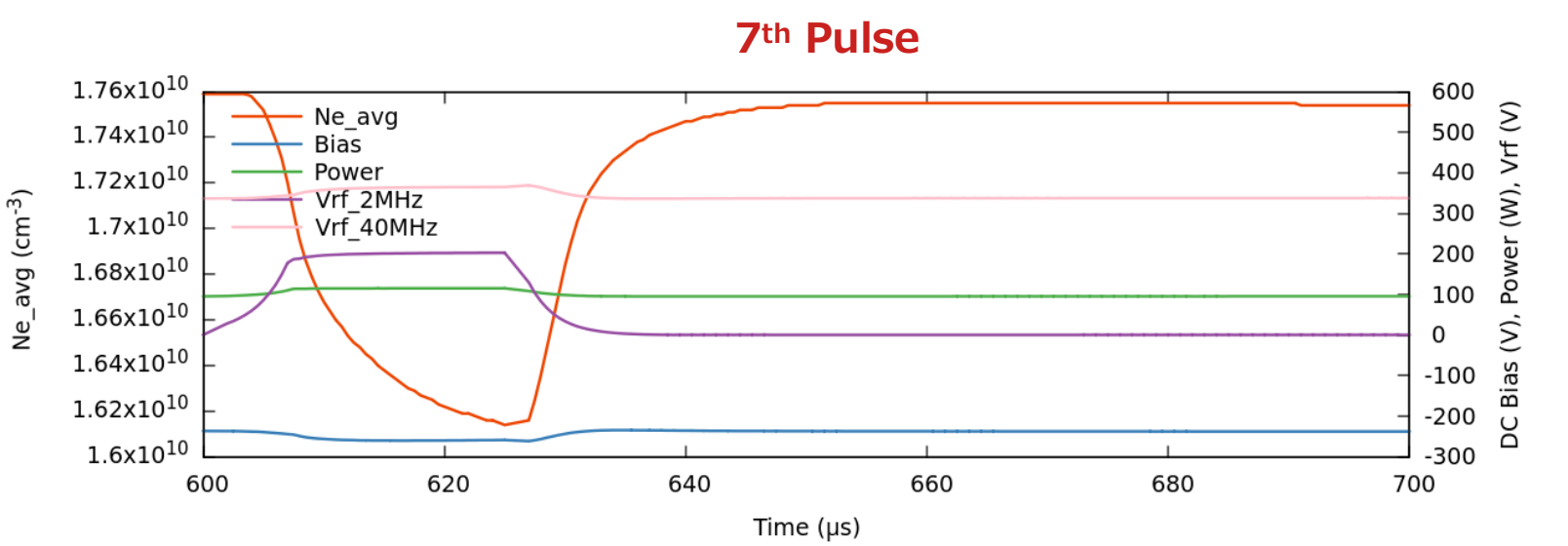
Fig. 7 パルス Duty 比 25% の場合の、第 7 パルス時の平均電子密度、DCバイアス、トータルパワー、
2 つの RF 周波数電圧の時間変化
プラズマ分布の時間変化(Duty 比 25%)
Fig. 8 は、パルス Duty 比 25% の場合の、電子密度分布、電子温度分布、イオン速度分布、平均電位分布の、第 7 パルス時における時間変化のアニメーションです。
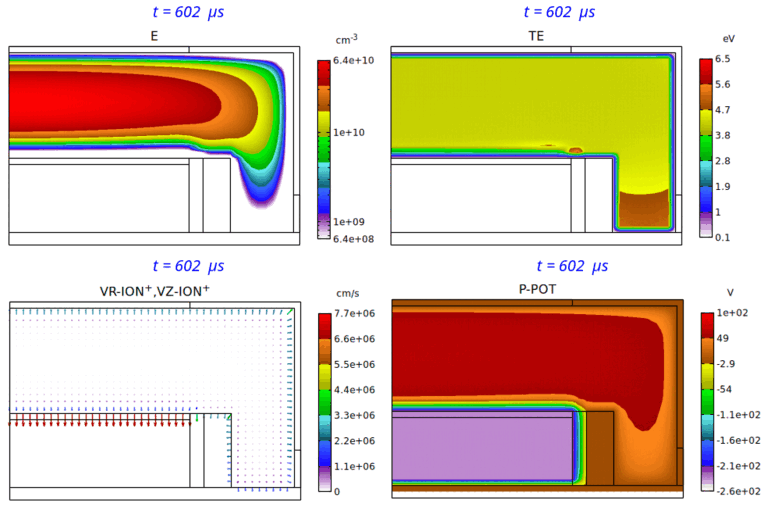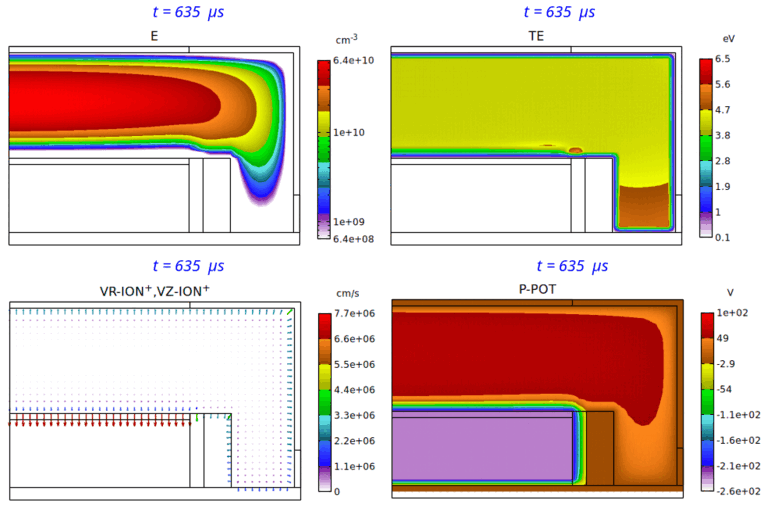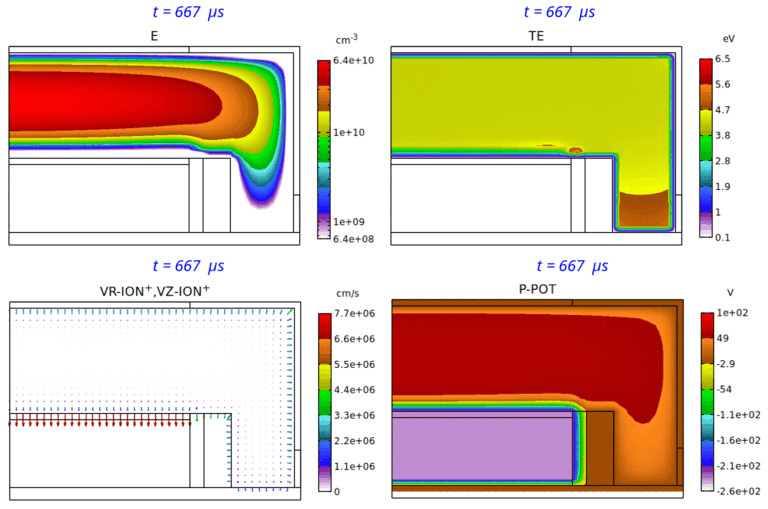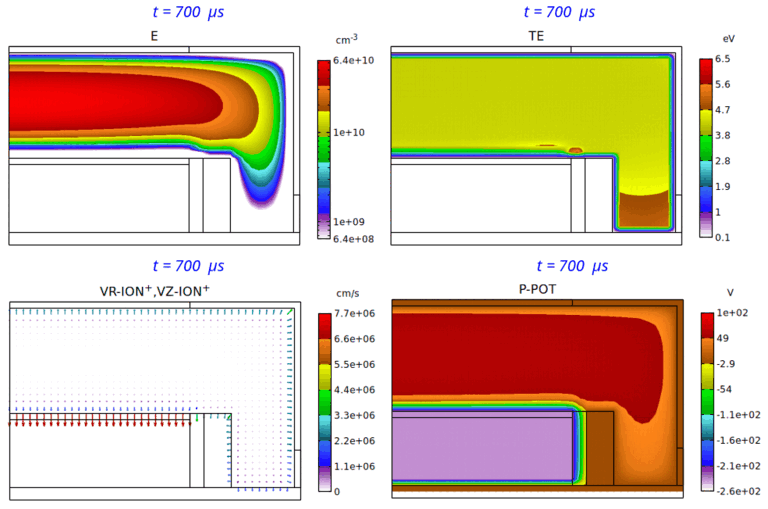
Fig. 8 パルス Duty 比 25% の場合の、電子密度 (E) 分布 ( 2-decade の対数スケール表示)、電子温度 (TE) 分布、
イオン速度 (VR-ION+,VZ-ION+) 分布、平均電位 (P-POT) 分布の時間変化
IEAD(Duty 比 25%)
Duty 比 25% の場合の IEAD も PCMC で計算しました。Fig. 9(a), (b) に ON-Pulse/OFF-Pulse 終了直前の瞬時 IEAD を、Fig. 9(c), (d) にON-Pulse/OFF-Pulse の位相平均 IEAD を示します。全体的に、Duty 比 50% の場合の IEAD とほとんど同じ IEAD が得られています。ただし、Fig. 9(d) に見られる高エネルギー側のテールは Duty 比 50% の Fig.5(d) に比べて小さくなっています。これは OFF-Pulse 時間が長くなったため、バルス電圧の立ち下がり遷移中の入射イオンの影響が相対的に小さくなったためと考えられます。
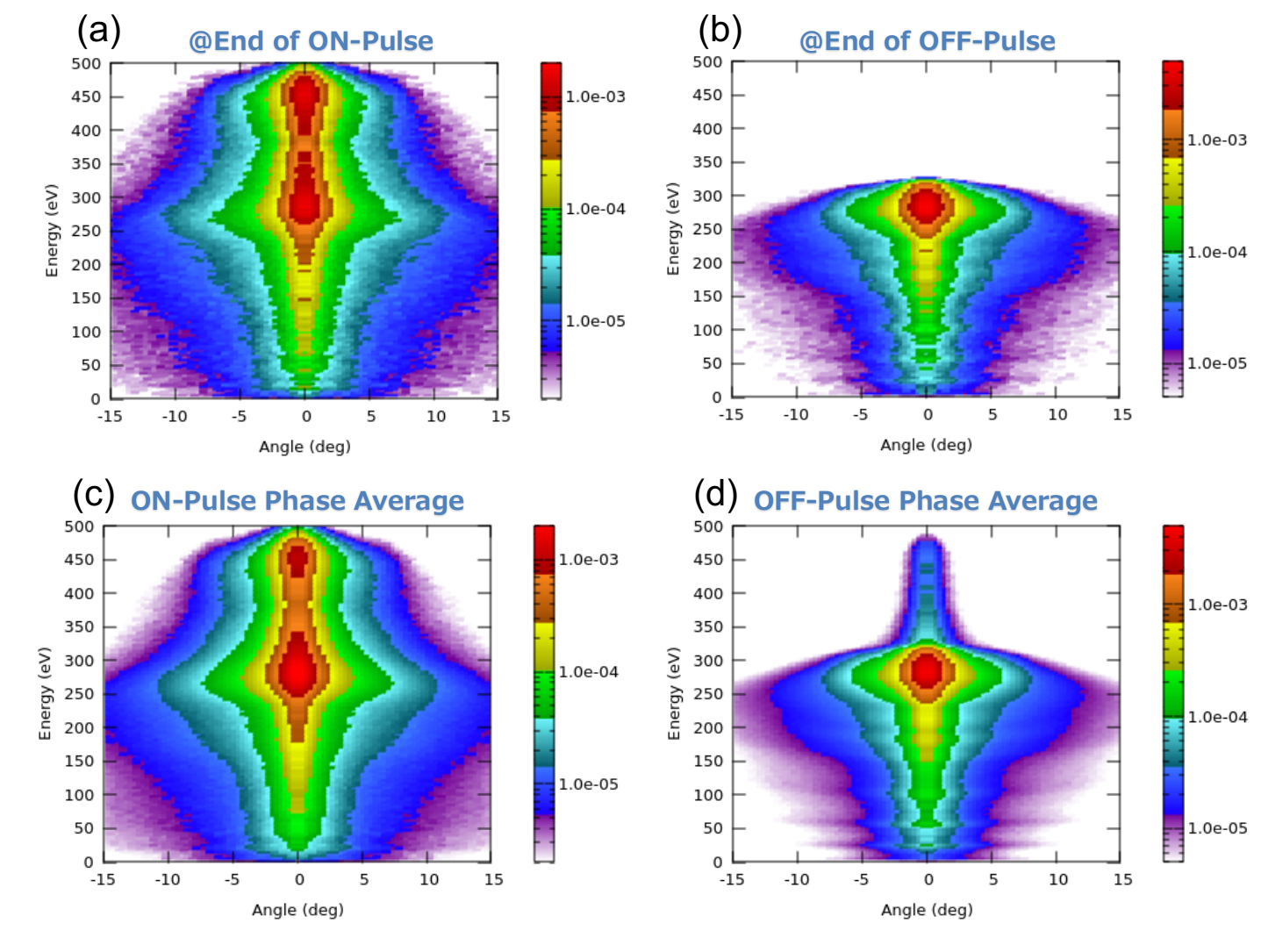
Fig. 9 パルス Duty 比 25% の場合の IEADs ( 3-decade の対数スケール表示) : ON-Pulse 終了直前の瞬時 IEAD (a)、
OFF-Pulse 終了直前の瞬時 IEAD (b)、ON-Pulse 位相平均 IEAD (c)、OFF-Pulse 位相平均 IEAD (d)
IEAD(Duty 50% と 25% の場合の比較)
パルス ON/OFF に渡って平均した、パルス周期平均 IEAD を算出し、その Duty 比依存を Fig. 10 に示します。基本的にどちらの IEAD も双峰型を示していますが、大まかには Duty 比に応じて低周波バイアスによる高エネルギー成分の割合が変化するような分布になっていると理解できます。
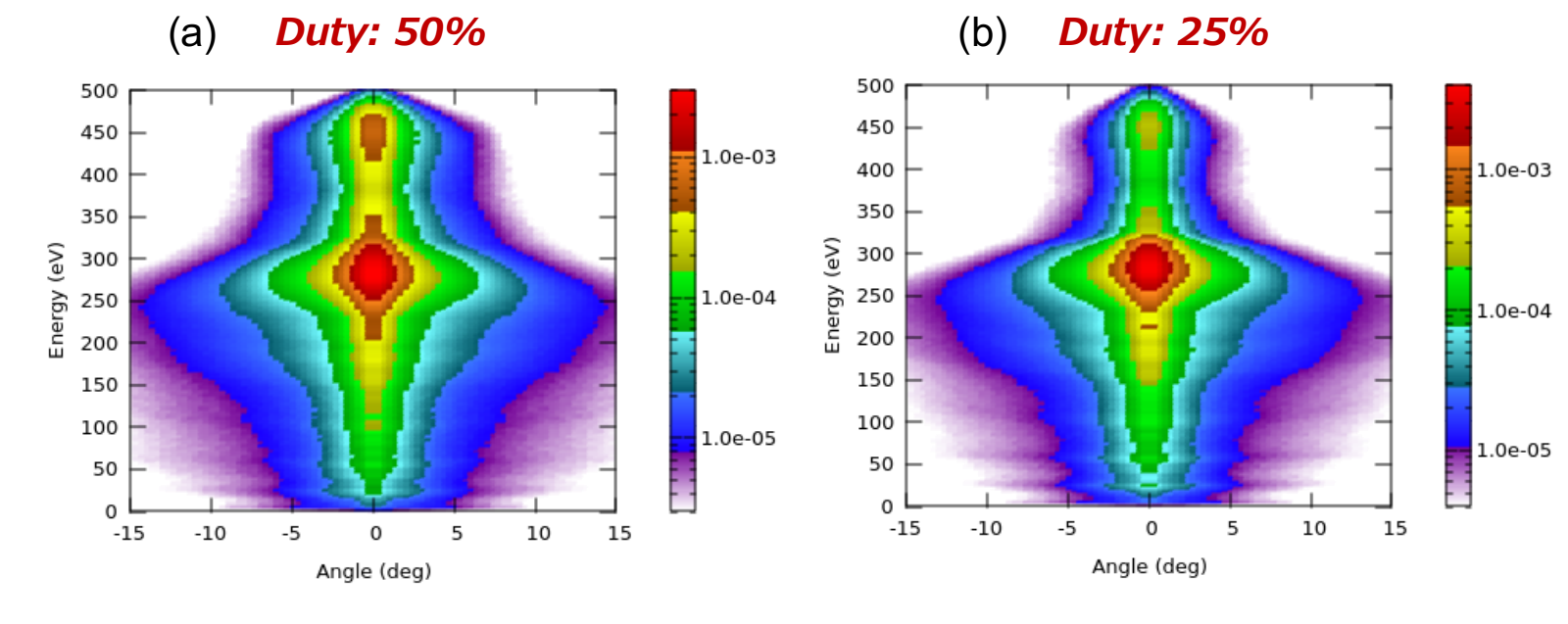
Fig. 10 パルス周期平均 IEADs ( 3-decade の対数スケール表示) :
Duty 比 50% の場合 (a)、 Duty 比 25% の場合 (b)
おわりに
Q-VT を用いて、低周波のみパルス変調した RF 2 周波重畳 CCP のシミュレーション例を紹介しました。粗いモデルで定性的ではありますが、本 CCP の特徴的な IEAD を可視化することができました。本稿が、Q-VT の機能を知っていただき、広く利用していただけるきっかけとなれば幸いです。
© 2008- ATHENASYS Co., Ltd. All Rights Reserved.
