はじめに
プロセスプラズマのシミュレーションツールとして、M. J. Kushner 教授により開発された HPEM (Hybrid Plasma Equipment Model) はあまりにも有名であり、これまでにHPEMを用いた数多くの研究成果が論文として発表されています。もともと HPEM は大学で開発されたものであり、使用に関しては計算設定のための膨大な数のパラメーターの意味を理解する必要があるため、一般企業などで使いこなすことは至難の業でした。英国の Quantemol 社は、容易にプラズマシミュレーションが実行できるように、HPEM のフロントエンドとなる グラフィカル ユーザー インターフェイス (GUI) を開発し、 HPEM と組み合わせて Q-VT (Quantemol-Virtual Tool) としてライセンス販売しています。
今回当社では Q-VT を用い、名古屋大学の論文(S. Kuboi, H. Kato, Y. Seki, H. Suzuki, and H. Toyota, Jpn J. Appl. Phys. 62, SI1003 (2023))に示されている装置を参考にして、パルス変調した RF 2 周波駆動の容量結合プラズマ (Pulse-Modulated Dual Frequency CCP) の計算を試みましたので簡単に紹介します。近年、パルス変調した RF 2 周波 CCP はエッチングなどのプロセス性能が良好なことから、プラズマプロセスでは頻繁に用いられています。異なる電極に異なる周波数の RF を印加するタイプがよく知られていますが、本例は同一電極に異なる周波数のRFを印加する CCP に関するものです。
もともと HPEM は定常状態のプラズマ計算に適したコードですが、パルス変調 CCP などの時間発展も近似的に追跡することも可能です。本稿ではパルス変調 CCP の数パルス間の過渡状態を計算しています。今回の計算では HPEM のリスタート機能を利用してパルスの ON/OFF を切り替えていますが、この操作を簡単化するため当社で独自開発した batres というツールを用いました。なお、上記文献ではプロセスガスとして C4F8 混合ガスが用いられていますが、本稿では簡単のため純 Ar ガスを用いて計算しています。
装置モデル・計算条件
上記文献に基づいて作成した装置形状モデル・計算用グリッドを Fig. 1 に示します。グリッド数は 43 × 33 と非常に粗くなっていますが、本稿の目的が Q-VT の機能の紹介であるため計算精度は犠牲にし、計算スピードを優先しました。このシステムは、直径 20 cm ウエハ用の円筒対称の容量結合プラズマ (CCP) 装置です。ウエハは、誘電体リング (比誘電率 8) に囲まれた RF 駆動電極上に置かれます。駆動電極には、ブロッキング コンデンサ(20 nF)を介して 40 MHz と 2 MHz の RF 電力が重畳され、さらにパルス変調されて供給されます。パルスの周波数は 1 kHz で Duty 比は 50% 、またパルス ON 時のパワーは 100 W (40 MHz) および 20 W (2 MHz) となるように各 RF 電圧が調整されます。この電極には DC バイアスが発生します。ウエハから 3 cm 上にあるシャワーヘッドからは、Ar ガスが 60 標準 cc/分 (sccm) で流入します。イオンの二次電子放出係数はウェハ表面で 0.05 としました。リアクタ内の圧力は 4 Pa で一定に、また装置全体が温度 52 °C に保たれています。また Q-VT では、計算グリッドの最外面にグランド電位のセルが自動的に配置されます。
計算条件としては、重粒子種に対するタイムステップ (1 iteration の時間) は 500 ns (2 MHz の 1 周期)としました(ちなみに Q-VT ではこのタイムステップを RF 1 周期以下に設定できません)。電子のタイムステップは HPEM 内部で自動調整され 62 ps 程度でした。HPEM では電子の輸送をモンテカルロ法により解くことも可能ですが、今回の計算では、電子の輸送は二項近似の Boltzmann 方程式に基づいて決定し、電子、イオン、中性ガス、それぞれについての質量保存式、運動量保存式、エネルギー保存式を近似的に解いてます。
実際の計算にあたっては、パルス ON の条件で 1000 iteration、パルス OFF の条件で 1000 iteration というように、条件を変更したリスタート計算を交互に繰り返しています。この操作を簡単化し一括処理するため batres というツール(コマンドライン上のスクリプト: 当社独自のもので英国 Quantemol 社とは無関係)を開発しました。今回の計算では、最初から 5 パルスまで(累計 10000 iteration)の CCP の時間発展を計算しています。これに要した計算時間は、OS: Ubuntu22 Linux、CPU: Core i9-12900 (2.4 GHz)、シングルコアの環境で約 18.6 時間でした。
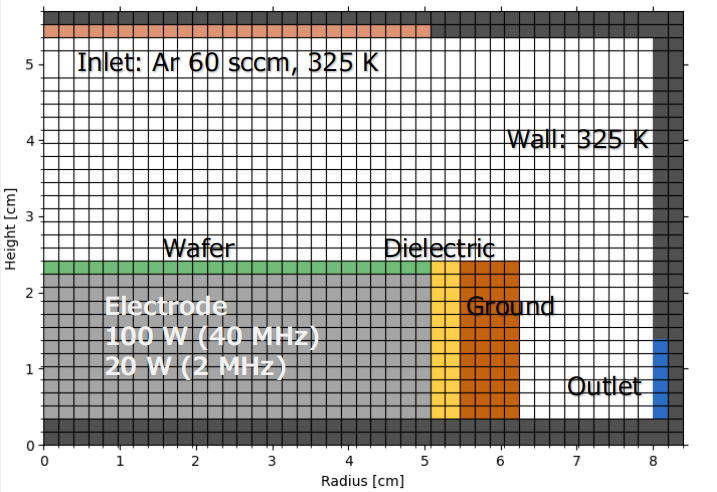
Fig. 1 装置形状モデル・計算用グリッド (グリッド数 43 ✕ 33)
反応モデル
考慮した化学種は、中性種として、 Ar, Ar* (* 付きは励起種)、イオン種として Ar+ です。今回使用した化学反応モデルを Fig. 2 に示します (HPEM では電子を含め元素名などはすべて大文字で表し、また正イオンを ' ^ ' 記号で、反応方向を表す矢印→を ' > ' 記号で表します)。ここで、A, n, E は反応速度を Arrhenius 式で表した場合のパラメータで、それぞれ反応速度定数、温度のベキ乗指数、活性化エネルギーです。A が 0 の反応は電子衝突反応で、HPEM 内蔵の電子衝突断面積が使用されます(内蔵データには特別な番号 special number が自動的に付与されています)。HPEM には主なガス種の電子衝突断面積データがハードコード(内蔵)されていて容易に利用することができます。 また壁における、励起種 Ar* の脱励起率は 1.0 としました。
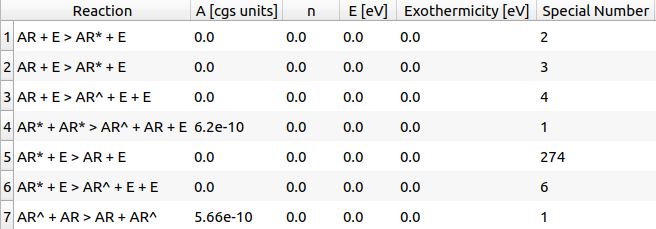
Fig. 2 反応モデル ( Q-VT 上での画面表示)
プラズマの時間発展
第 5 パルスまでの、平均電子密度、DCバイアス、トータルパワー、2つのRF周波数電圧の時間発展の様子を Fig. 3(a) に示します。また Fig. 3(b) に平均電子密度と平均ガス温度の時間発展を示します。パルスの ON/OFF に伴い、プラズマが生成・減衰を繰り返す様子が明瞭に再現されています。また 5 パルスではまだ収束(周期定常状態)には至っておらず、各パラメータは徐々に増加していることがわかります。さらに計算を続行することも可能ですが、今回はここで打ち切りました。それでも 5 パルスで、かなり周期定常に近い状態まで達していることが伺えます。
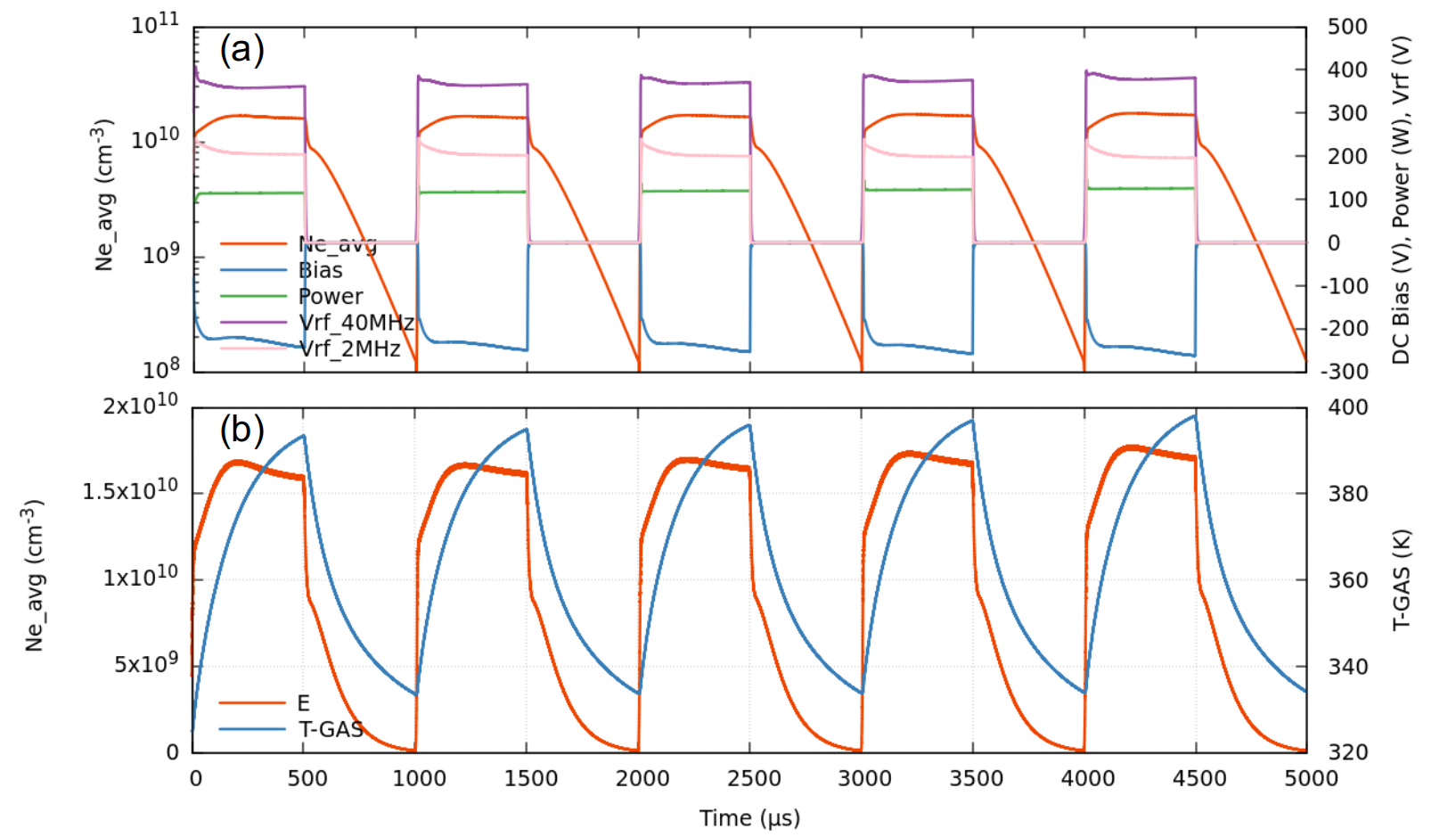
Fig. 3 平均電子密度、DC バイアス、トータルパワー、2つの RF 周波数電圧 (a)
及び 平均電子密度、平均ガス温度 (b) の時間発展の様子
Fig. 4 に第 5 パルス時の様子を拡大表示しました。今回の計算ではパルス ON 直後、 RF 電圧、パワーには若干のオーバーシュートが見られますが、DC バイアスには大きなオーバーシュートは見られず、電子密度も滑らかに増加しています。パルス電圧の立ち上がり時間はおおよそですが 10 μs 程度でした。なお、HPEM の PCMC (Plasma Chemistry Monte Carlo) モジュールを利用して追加の計算をすれば、任意の時点でのイオンエネルギー分布を算出することも可能ですが、今回はそこまで行っていません。
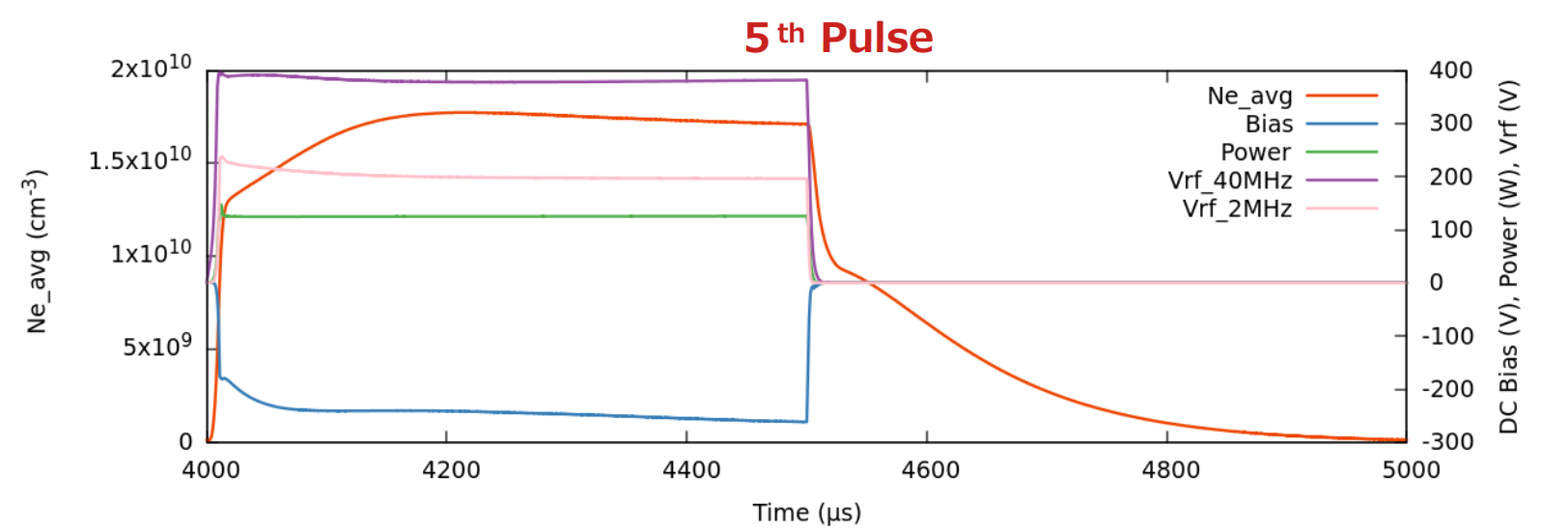
Fig. 4 第 5 パルス時の平均電子密度、DCバイアス、トータルパワー、2 つの RF 周波数電圧の時間変化
プラズマ分布の時間変化(第 5 パルス時)
Fig. 5 は、電子密度分布、電子温度分布、パワー密度分布、ガス温度分布の、第 5 パルス時における時間変化のアニメーションです。RF 2 周波パルス変調 CCP の特徴を具体的・視覚的に理解するのに役立つものと思われます。
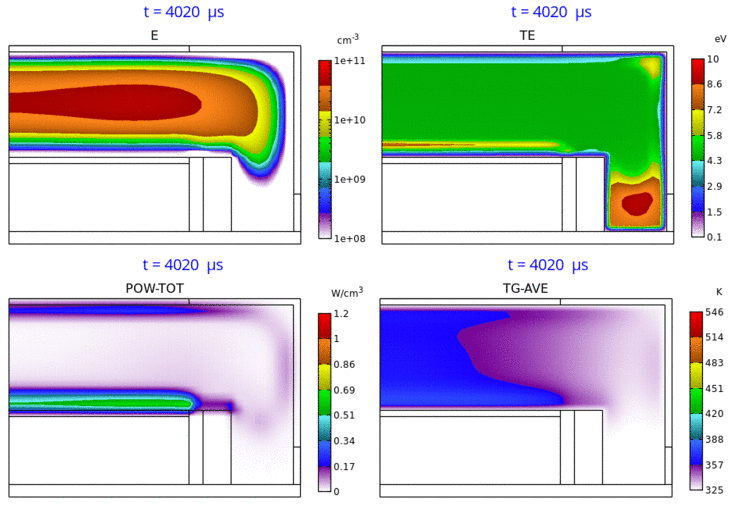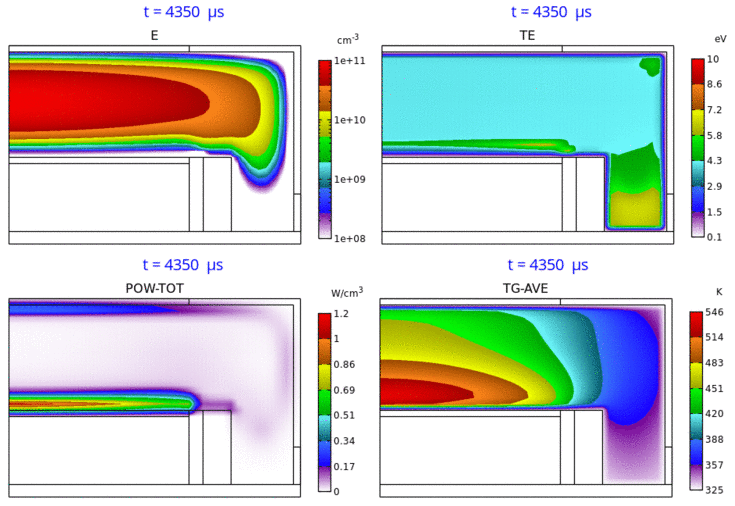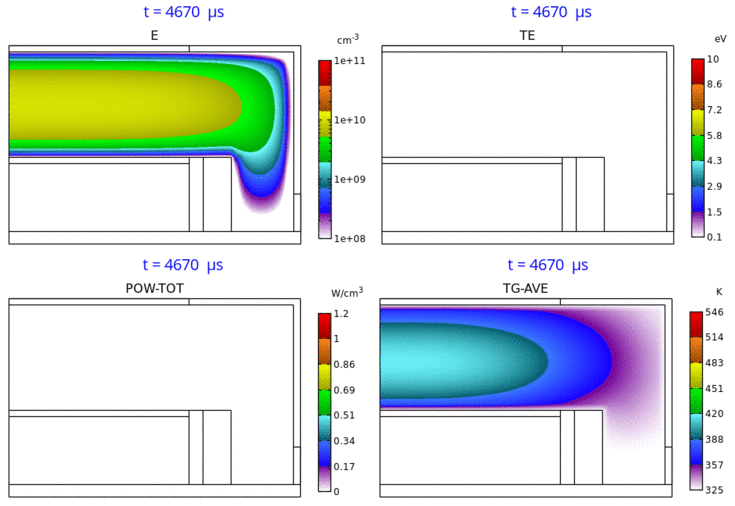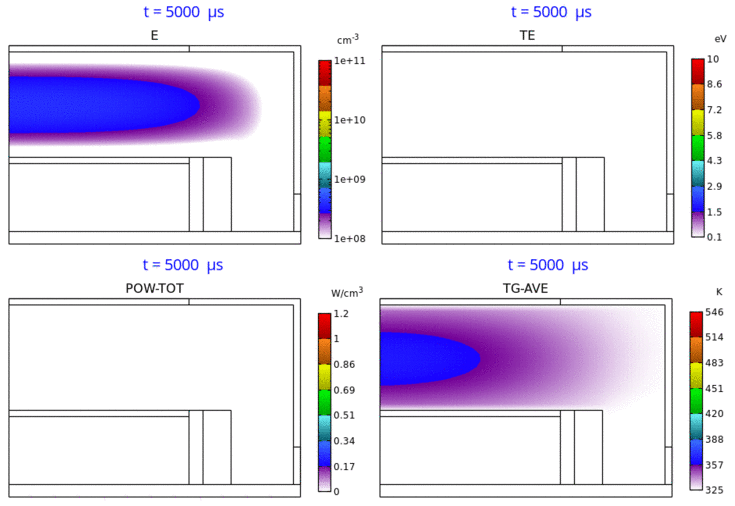
Fig. 5 電子密度 (E) 分布 ( 3-decade の対数スケール表示)、電子温度 (TE) 分布、パワー密度 (POW-TOT) 分布、
ガス温度 (TG-AVE) 分布の時間変化
おわりに
Q-VT を用いた RF 2 周波パルス変調 CCP シミュレーション例を紹介しました。非常に粗いモデルですが、パルス変調 CCP の特徴を定性的に再現できたと思います。本稿が、Q-VT の機能を知っていただき、広く利用していただけるきっかけとなれば幸いです。
© 2008- ATHENASYS Co., Ltd. All Rights Reserved.
