はじめに
プロセスプラズマのシミュレーションツールとして、M. J. Kushner 教授により開発された HPEM (Hybrid Plasma Equipment Model) はあまりにも有名であり、これまでにHPEMを用いた数多くの研究成果が論文として発表されています。もともと HPEM は大学で開発されたものであり、使用に関しては計算設定のための膨大な数のパラメーターの意味を理解する必要があるため、一般企業などで使いこなすことは至難の業でした。英国の Quantemol 社は、容易にプラズマシミュレーションが実行できるように、HPEM のフロントエンドとなる グラフィカル ユーザー インターフェイス (GUI) を開発し、 HPEM と組み合わせて Q-VT (Quantemol-Virtual Tool) としてライセンス販売しています。
今回当社では、近年発表された下記論文を参考にして、PE-ALD (Plasma-Enhanced Atomic Layer Deposition) 用の容量結合プラズマ (CCP) の Q-VT による計算を試みましたので簡単に紹介します。PE-ALD プロセスでは、原料ガスのウエハ表面への吸着ステップとプラズマで生成される活性種を利用したウエハ表面反応ステップを交互に繰り返しますが、本稿は後者のステップで利用される CCP の定常状態に関する計算になります。
参照論文: C. Qu, Y. Sakiyama, P. Agarwal, and M. J. Kushner, J. Vac. Sci. Technol. A 39, 052403 (2021)
装置モデル・計算条件
上記 Qu らの論文に基づいて作成した装置形状モデル・計算用グリッドを Fig. 1 に示します。このシステムは、直径 30 cm のウエハを処理するために設計された円筒対称の容量結合プラズマ (CCP) 装置です。ウエハは、石英 (比誘電率 4.0) フォーカス リングに囲まれた接地基板上に置かれます。ウエハから 1.5 cm 上にある上部電極には、ブロッキング コンデンサを介して 10 MHz の RF 電力が供給され、DC バイアスが発生します。入力電力は上部電極に印加する電圧 Vrf を変えることによって 500 W に調整されます。シャワー ヘッドは上部電極を兼ねていて、Ar/O2 = 80/20 混合ガスが 5 標準リットル/分 (slm) で流入します。イオンの二次電子放出係数は、プラズマにさらされるすべての表面で 0.05 です。リアクタ内の圧力は 2 Torr で一定に保たれ、基板とフォーカス リングの温度は 50 °C 、その他の表面の温度はすべて 25 °C です。また Q-VT では、計算グリッドの最外面にグランド電位のセルが自動的に配置されます。
計算条件としては、重粒子種に対するタイムステップ (1 iteration の時間) は 200 nsとしました。電子のタイムステップは HPEM 内部で自動調整され 0.1 ns 程度でした。HPEM では電子の輸送をモンテカルロ法により解くことも可能ですが、今回の計算では、電子の輸送は二項近似の Boltzmann 方程式に基づいて決定し、電子、イオン、中性ガス、それぞれについての質量保存式、運動量保存式、エネルギー保存式を近似的に解いてます。
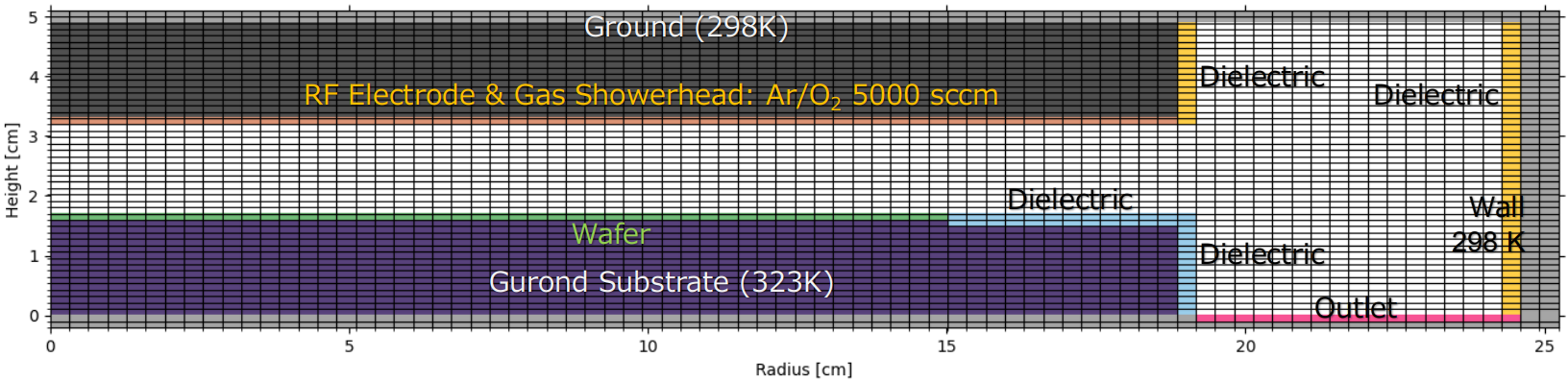
Fig. 1 装置形状モデル・計算用グリッド (グリッド数 79 ✕ 50)
反応モデル
考慮した化学種は、中性種として、 Ar, Ar*, O2, O2*, O, O* (* 付きは励起種)、イオン種として Ar+, O2+, O-です。今回使用した化学反応モデルを Fig. 2 に示します (HPEM では電子を含め元素名などはすべて大文字で表し、また正イオンを ' ^ ' 記号で、反応方向を表す矢印→を ' > ' 記号で表します)。ここで、A, n, E は反応速度を Arrhenius 式で表した場合のパラメータで、それぞれ反応速度定数、温度のベキ乗指数、活性化エネルギーです。A が 0 の反応は電子衝突反応で、HPEM 内蔵の電子衝突断面積が使用されます(内蔵データには特別な番号 special number が自動的に付与されています)。HPEM には主なガス種の電子衝突断面積データがハードコード(内蔵)されていて容易に利用することができます。
また壁における、励起種の脱励起率は、0.5 (O2*), 0.1 (O*), 1.0 (Ar*)、また O 原子の O2 への再結合率は 0.05 としました。
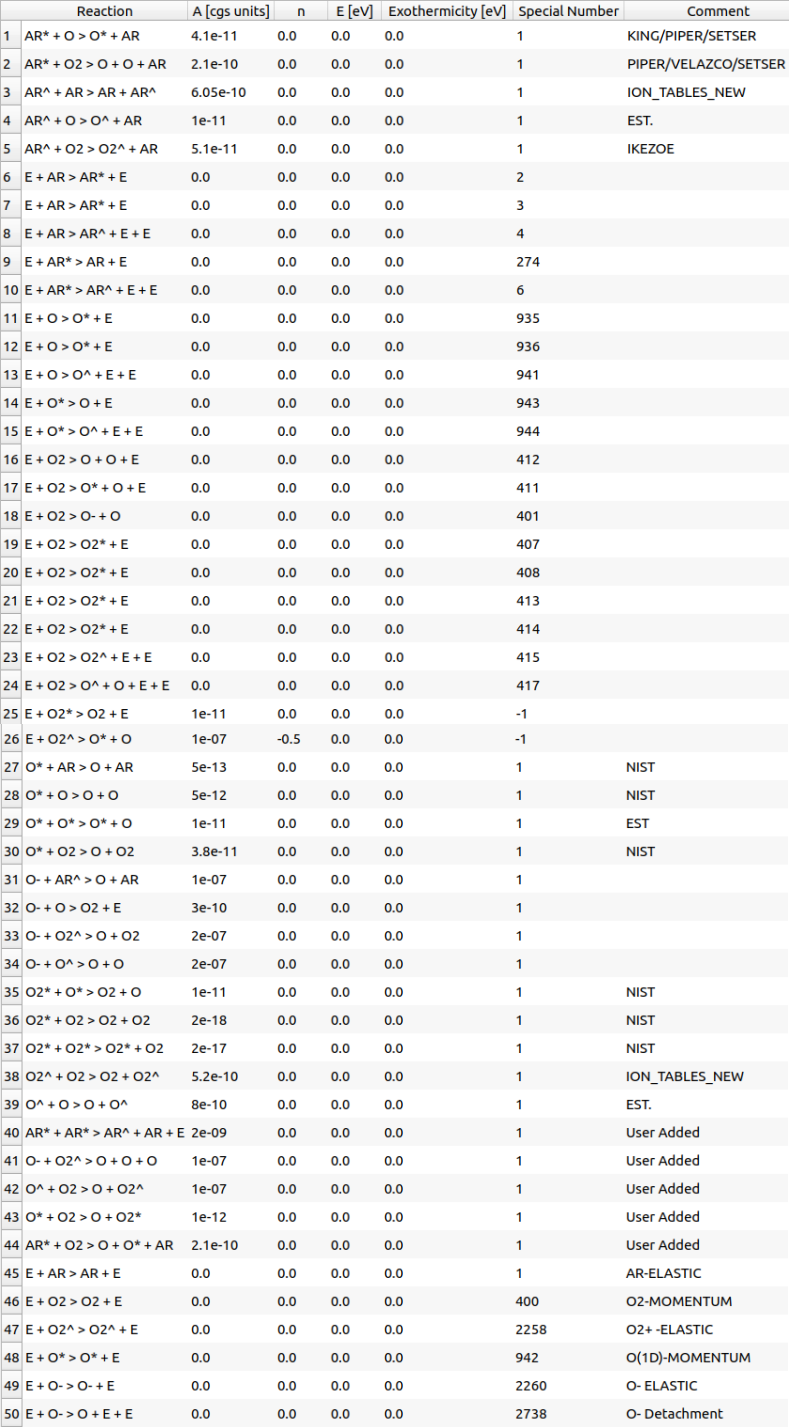
Fig. 2 反応モデル ( Q-VT 上での画面表示)
イオン・中性ガス衝突断面積
PE-ALD の表面反応ステップでは、ウエハに入射するイオンのエネルギーを適切に制御する必要があります。このイオンのエネルギーを正確に計算するためにイオン・中性ガス衝突の断面積のエネルギー依存性が重要となります。少し細かい話になりますが、HPEM による計算では、このエネルギー依存性を決める TT0 というパラメータを適当な値に設定する必要があります。HPEM で想定している断面積のエネルギー依存性がこのパラメータによりどう変化するかを Fig. 3 に示します。Lieberman & Lichtenberg のテキスト "Principles of Plasma Discharges and Material Processing" 2nd ed., John Wiley & Sons, Inc.(2005) p. 77 のFIGURE 3.15 を参照すると TT0 = 106 程度が適当であると判断できます。
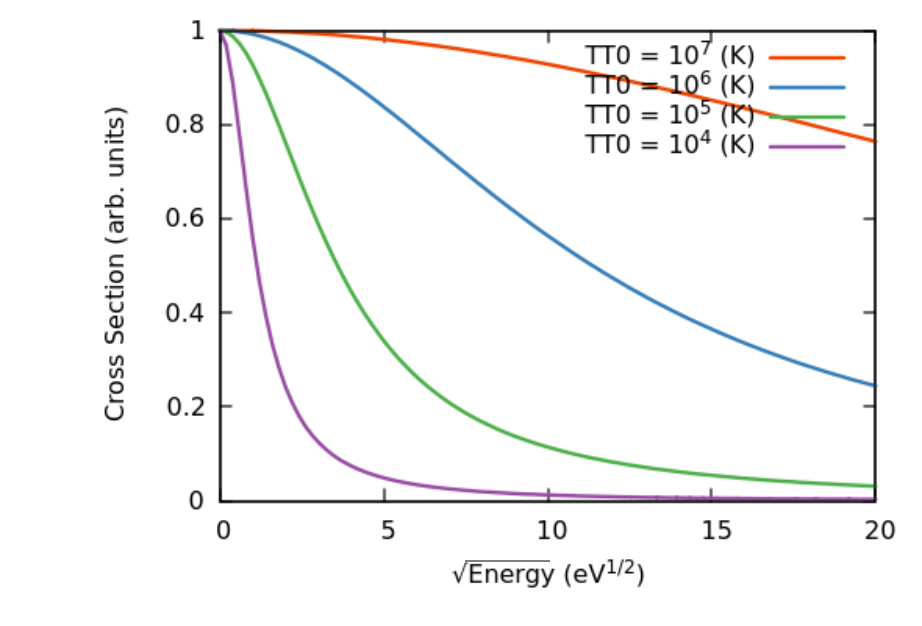
Fig. 3 イオン・中性ガス衝突の断面積のエネルギー依存性のモデル
計算の収束の様子
1000 iterationまで計算した場合の、中性種密度、荷電粒子密度、RF電圧、DCバイアスの変化を Fig. 4 に示します。最初の 400 iterations は HPEM の加速計算機能を使用しました。厳密にはまだ十分な精度までの収束には至っていませんが、更に iteration を追加しても結果に大きな変化はありませんでした。なお、1000 iteration までの計算時間は、OS: Ubuntu22.04 Linux、CPU: Core i9-12900 (2.4 GHz)、シングルコアの計算で 2時間35分でした。
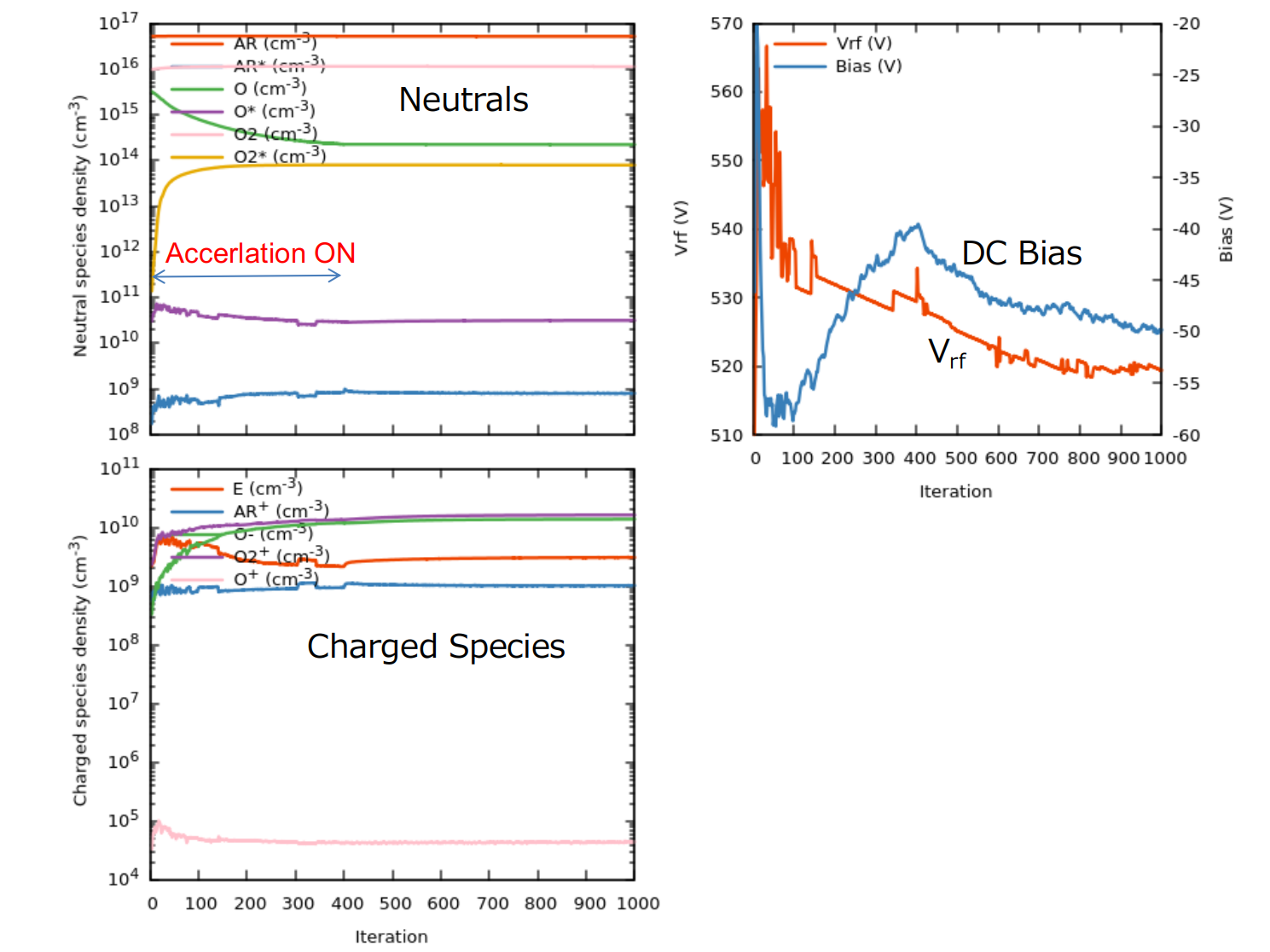
Fig. 4 中性種密度、荷電粒子密度、RF電圧 Vrf、DCバイアスの収束の様子
(E は電子を表す)
計算結果
Fig. 5 にO2 ガス分子のフラックス分布を示します。
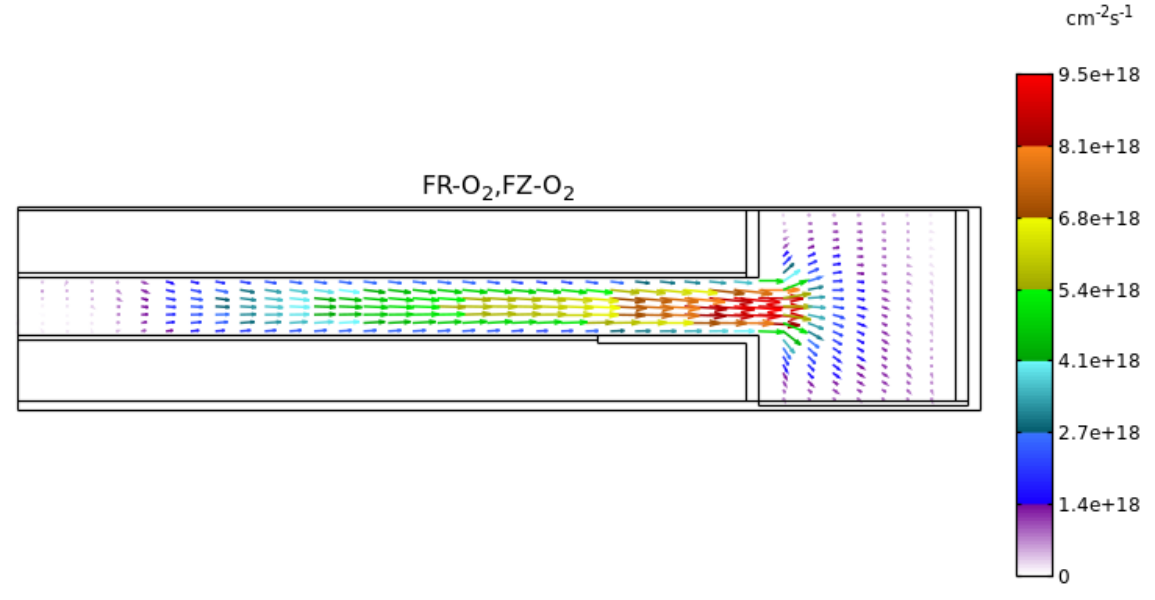
Fig. 5 O2 フラックス分布
Fig. 6 に電子密度分布を示します。
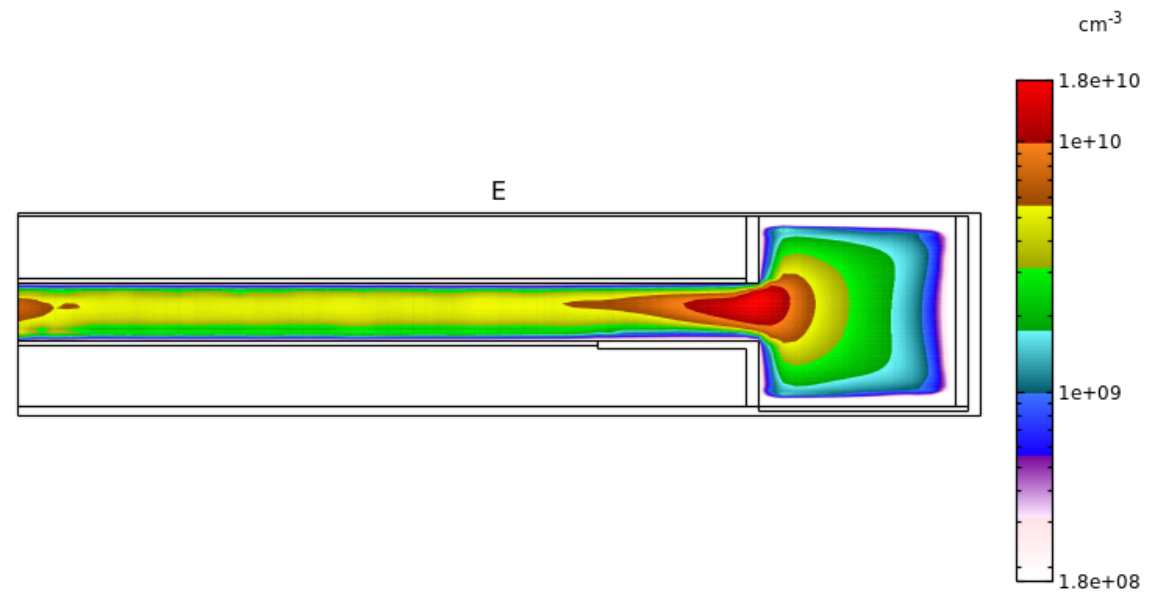
Fig. 6 電子密度分布 (2-decade の対数スケール表示)
Fig. 7 にO2+ 密度分布を示します。
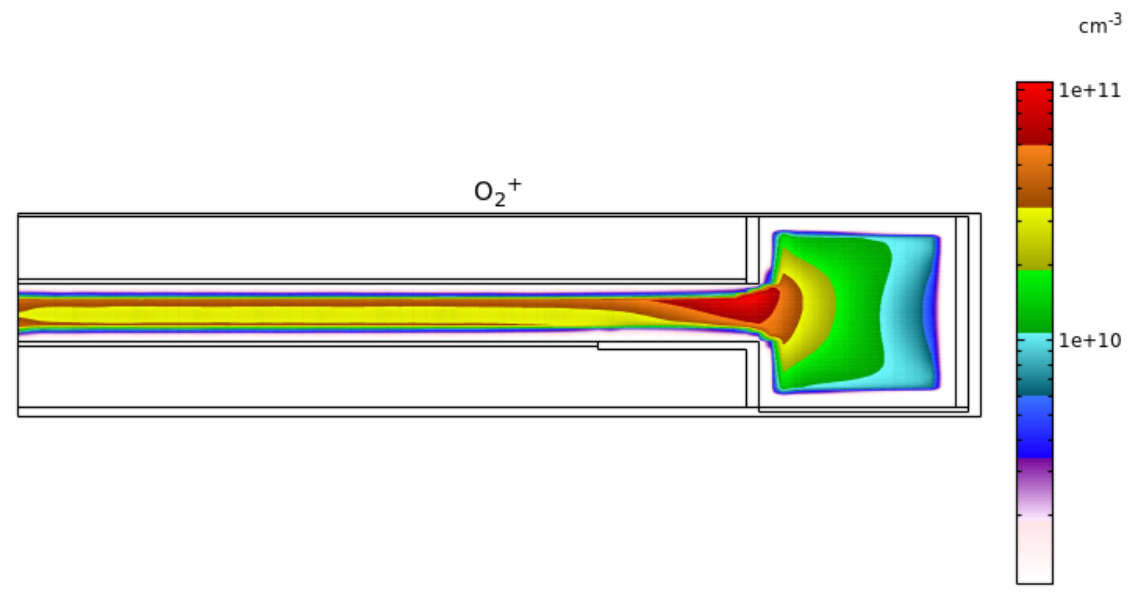
Fig. 7 O2+ 密度分布 (2-decade の対数スケール表示)
Fig. 8 にO- 密度分布を示します。
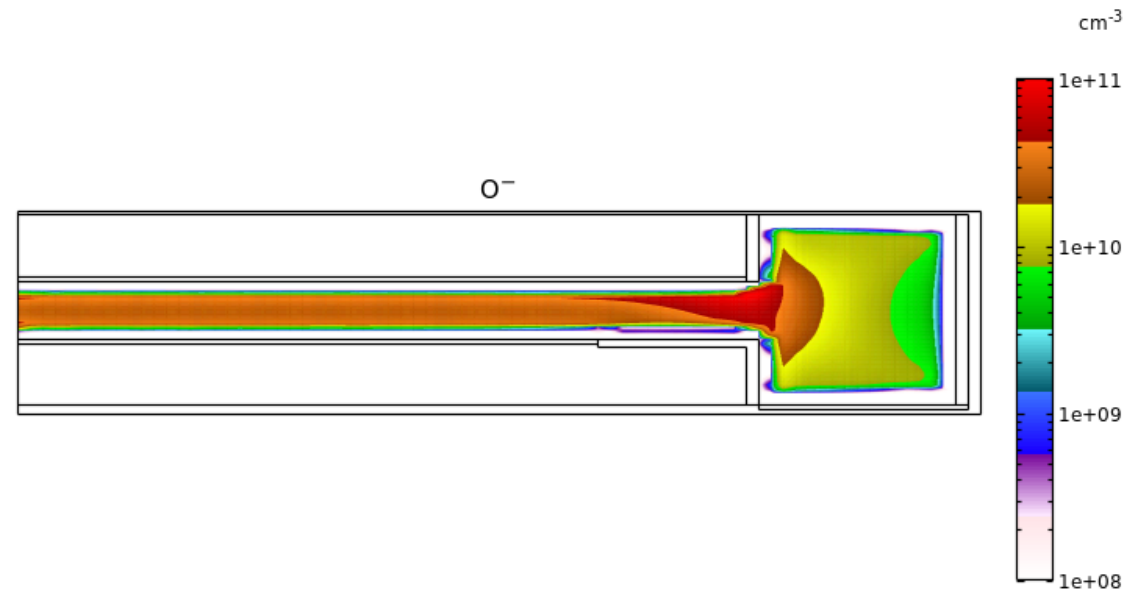
Fig. 8 O- 密度分布 (3-decade の対数スケール表示)
上記のプラズマ空間分布の計算結果に基づいて、ウエハに入射するイオン・中性粒子のエネルギー・角度分布をモンテカルロ法で計算しました。これには HPEM の PCMC (Plasma Chemistry Monte Carlo) モジュールを利用しています。Fig. 9 に、ウエハ半径中央位置における入射 Ar+, O2+, および O 原子のエネルギー・角度分布を示します。ALD に適した、10 − 20 eV 程度のイオン入射が予測されます。なお、 PCMC の計算時間は、3種類の粒子に対して各セルから放出するモンテカルロ粒子数が 2000 − 4000 個という条件で、2時間25分でした。
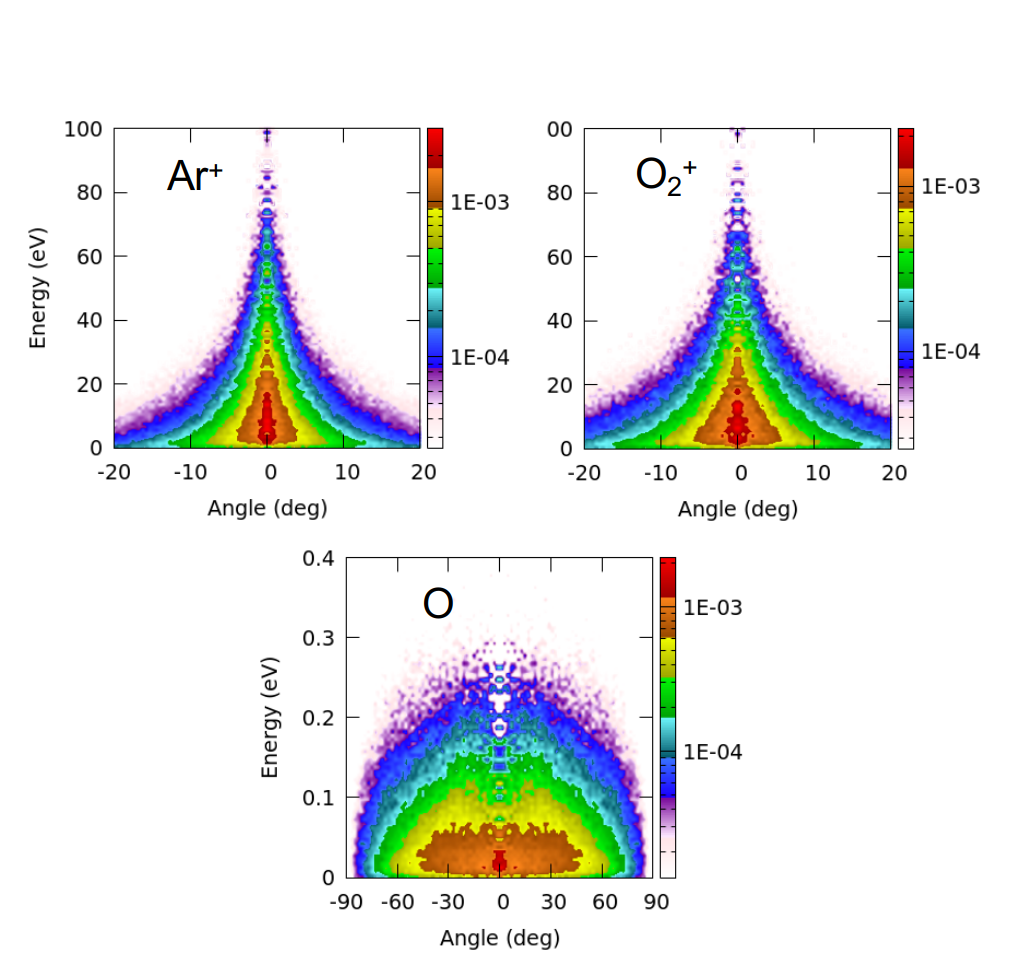
Fig. 9 入射 Ar+, O2+, および O 原子のエネルギー・角度分布 (2-decade の対数スケール表示)
おわりに
Q-VT を用いた PE-ALD 用 CCP シミュレーション例を紹介しました。参照した Qu らの論文の結果と比べると細かな差はありますが、類似した結果が得られています。本稿が、Q-VT の機能を知っていただき、広く利用していただけるきっかけとなれば幸いです。
© 2008- ATHENASYS Co., Ltd. All Rights Reserved.
