( ICP true transient simulation at the ignition )
プラズマの着火は,装置を開発する立場からはしばしば重要な問題となります.安定して再現性よく放電がスタートするかどうかは自明ではなく,異常放電が起きにくくしたり,安定して放電開始が出来るようにするために,様々な工夫が施されるのが一般的です.また,低圧高密度プラズマを用いた Etching プロセス等では,圧力が精度よく制御されているにも関わらず,放電開始直後には圧力が一瞬変動します(筆者自身の経験ですが).更には,放電開始時(着火時)には,いったいどのような現象が起きているのか,という素朴な疑問もあります.
ICP Simulatiom の多くは,周波数領域( frequency domain )による計算を行うことにより,周期定常状態を求めます.この方法では,1周期の間に掛かる平均的なエネルギーを計算し,定常計算によって解を求めるので,計算時間も短く,広く用いられている方法です.しかし,放電開始時に何が起きているかをシミュレーションによって検討・理解するには,非定常の解析が必要となります.
時間領域( time domain )によるプラズマのシミュレーションでは,プラズマ生成の様子を非定常で解析することが可能です.しかしながら,非常に小さな time step を用いる必要があることから,膨大な計算時間が掛かるという問題があります.以下では,非常に長い計算時間を要した結果ですが,放電開始の様子についてご紹介致します.
☆
始めに,計算モデルの概略を Fig. 1 に示します.
ガスは,Ar が上部から流入し,サセプターの周囲から排気されると仮定しています.RF電力は,2ターンのコイルによって供給されます(周波数:13.56MHz).サセプターは,8インチ基板よりもやや大きい寸法としています.
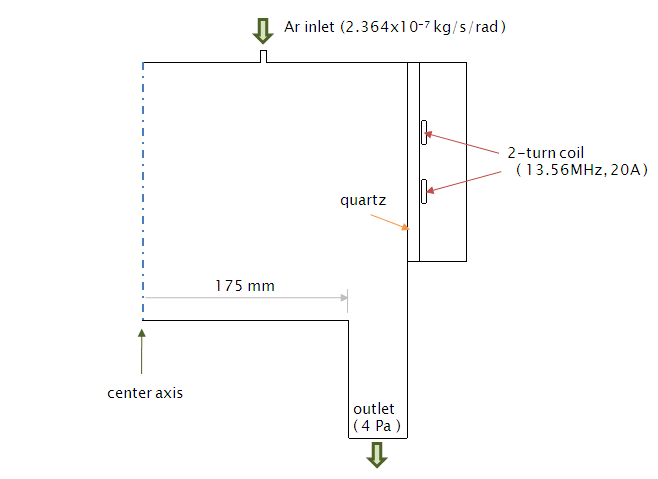
Fig. 1 計算モデル(二次元軸対称)
☆
計算結果は,option の選び方によって定量的には異なった結果となりますが,計算時間を少しでも短くするために,以下のような比較的簡易な option を用いました.
viscosity : Sutherland's law
specific heat : Consant ( 520 J/kg-K )
thermal conductivity : Prandtl Number ( 0.707 )
mass diffusitivity : Schmit Number ( 0.7 )
mobility : From Diffusivity
ion diffusion : same as neutrals
以下に,計算結果の一例を示します.
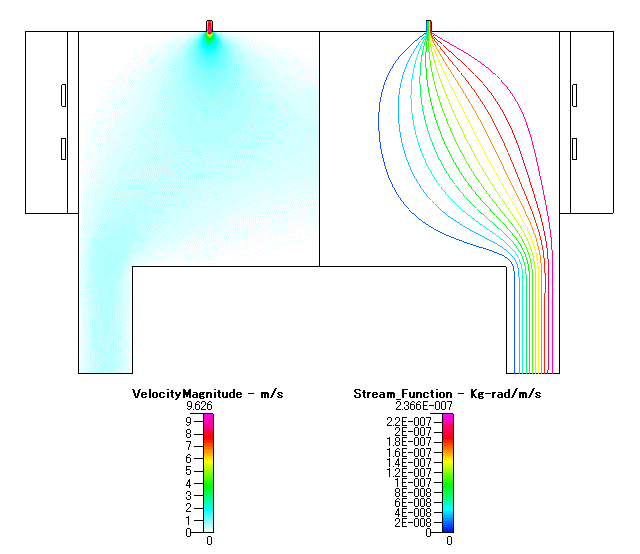
Fig. 2 流速分布( velocity mangnitude ) 及び 流れ関数( stream function )
流れの速い領域は,ガスの流入部付近のみとなっています.また,流れは典型的な層流です.
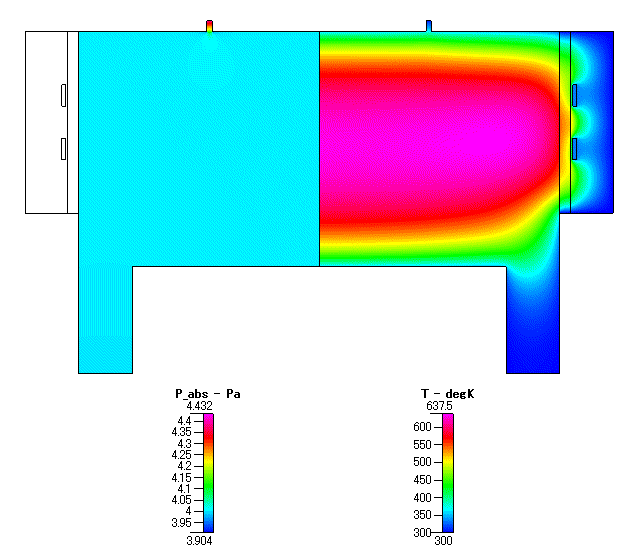
Fig. 3 絶対圧力 ( absolute pressure ) 及び 温度( gas temperature )
圧力は,チャンバー内の広い範囲でほぼ同じ圧力に維持されており,ガスの流入部付近でのみ,やや高い圧力になっていることが分かります.ガス温度は,プラズマ中心では壁面( 300K )と比べて 300K 以上高い値を示しています.ガスの密度は,理想気体 ( ideal gas law ) を仮定して計算していますが,温度が倍以上,ということは,数密度は 300K の壁面近傍の半分にまで減っていることを意味します.
CFD-ACE+ では,反応モデルの中に momentum transfer ( elastic collision ) のステップを含めることにより,ガスの温度上昇を加味することが可能です.本モデルでは,このステップを考慮し,更に,壁の slip ( Kn 数が 1 に近い条件で生じる壁でのスリップ)を考慮しています.
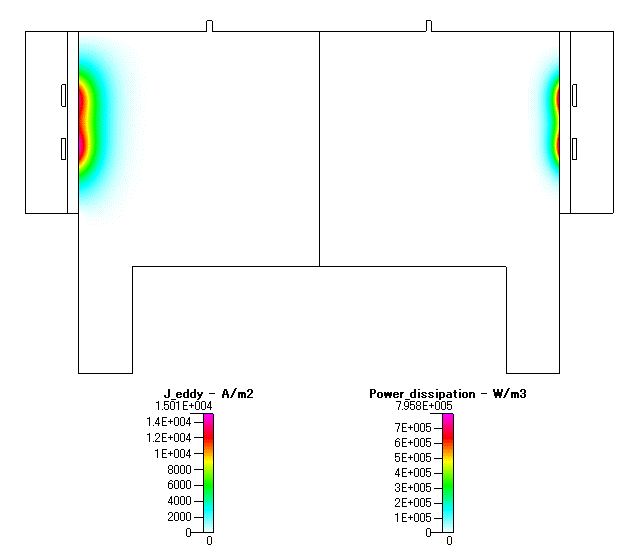
Fig. 4 渦電流( J_eddy )及び 吸収電力 ( Power dissipation )
明らかに,コイルに近い領域に偏っていることを示しています.
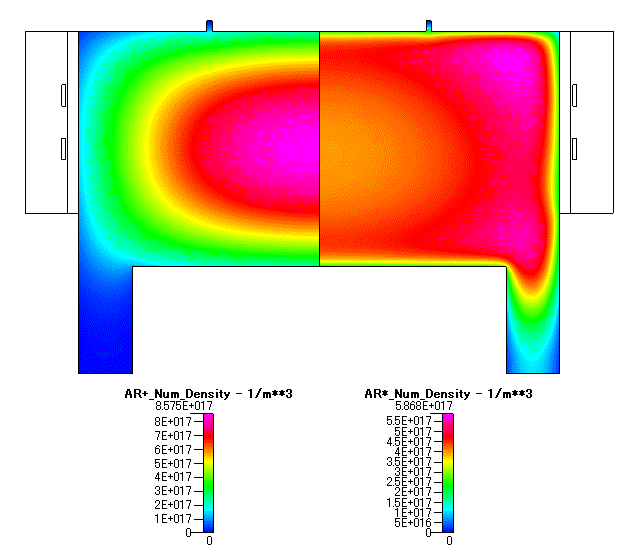
Fig. 5 Ar+ の数密度( AR+ number density ) 及び Ar* の数密度( Ar* number density )
Ar+ イオンは,プラズマの中央で高い一方で,励起準位の Ar* は,プラズマ密度の高い領域の外側で高くなる傾向を示しています.なお,本プラズマシミュレーションでは,両極性拡散を仮定した計算手法を用いているため,電子密度の分布と Ar イオン密度の分布は同じ結果となります.
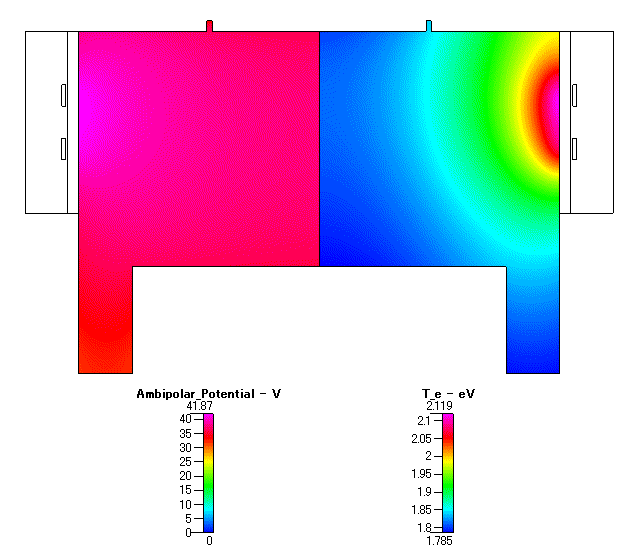
Fig. 6 両極性電位( ambipolar potential ) 及び 電子温度 ( Te )
電位分布の結果は,広い領域で 35〜 40V 程度,電子温度は,アンテナ近傍で最も高く,おおそ 2.1eV という結果になりました.
☆
次に,非定常計算の結果を示します.なお,計算中,Ne や Te がどのような変化をするかをモニターしてみました.
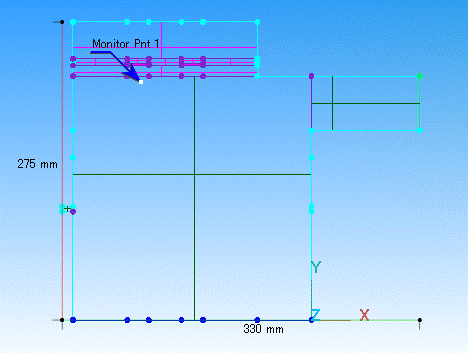
Fig. 7 モニターした position
得られた時刻歴は,以下のようになっています.
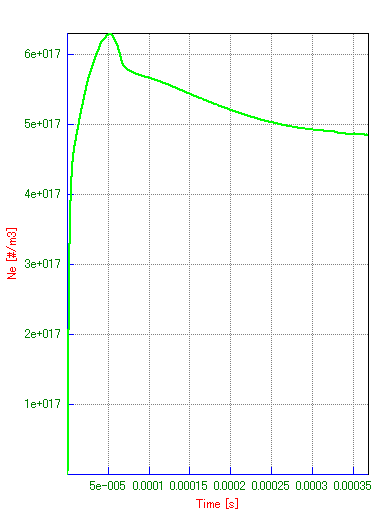
Fig. 8 Ne の時刻歴
Ne の値は,一度最大値に到達した後,やや下がることが分かります.
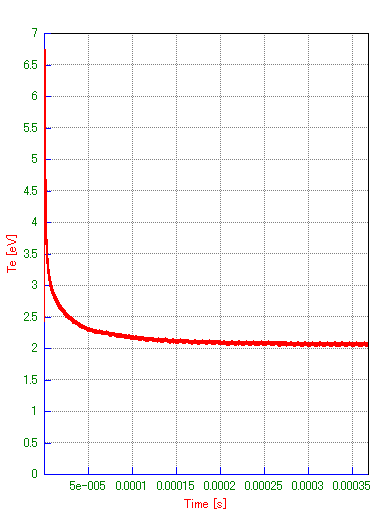
Fig. 9 Te の時刻歴
Te の値は,放電直後にかなり高い値を示しますが,急激に現象し,その後ゆっくりと定常状態に近づくことが分かります.
以下に,放電直後の 500step,及び,5000step の結果を示します.
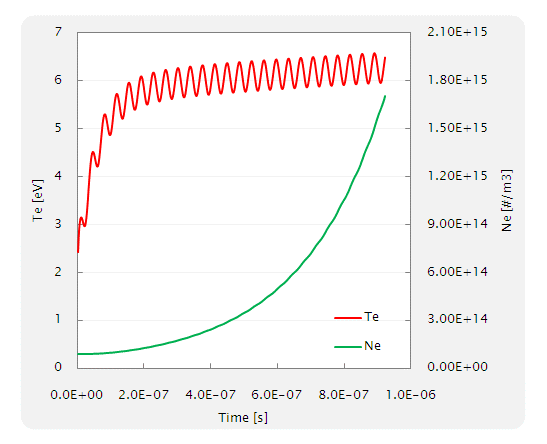
Fig. 10 Ne 及び Te の時刻歴(計算開始後の 500step の結果)
Te は,最初の数周期で 6eV 前後に到達し,その後,Ne がゆっくり上昇を始めることが分かります.
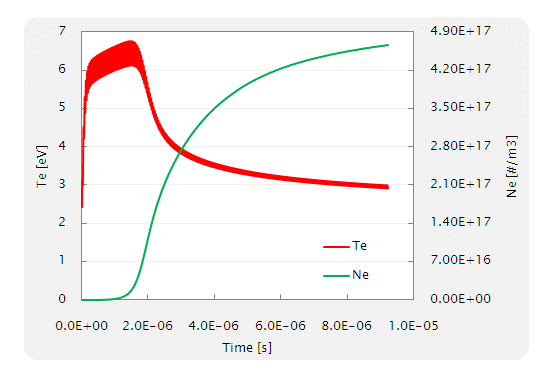
Fig. 11 Ne 及び Te の時刻歴(計算開始後の 5000step の結果)
Te は,最大で 7eV 弱まで上昇していますが,Ne の値が17乗のオーダーに到達するのは,すでに Te が 5eV 前後まで下がった後だということが分かります.このように,Te は短い時間で急激な変化をしますが,Ne の値は,電子温度に比べてゆっくり変わることが分かりました.
さて,以下に,プラズマが成長しながら,徐々にチャンバーの中央へと向う様子を示すアニメーションを示します.
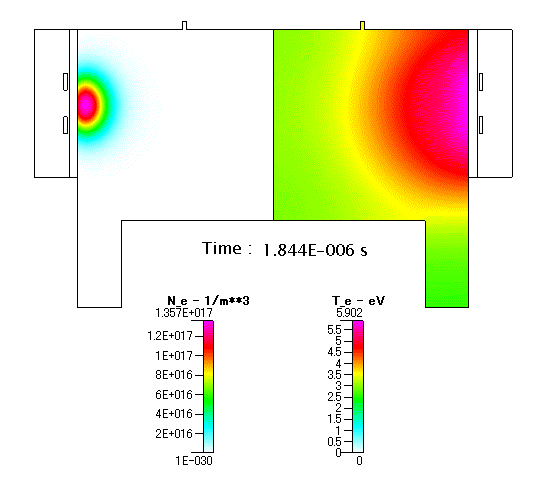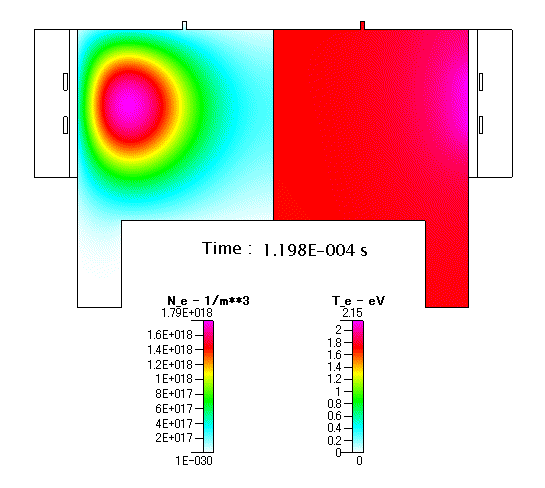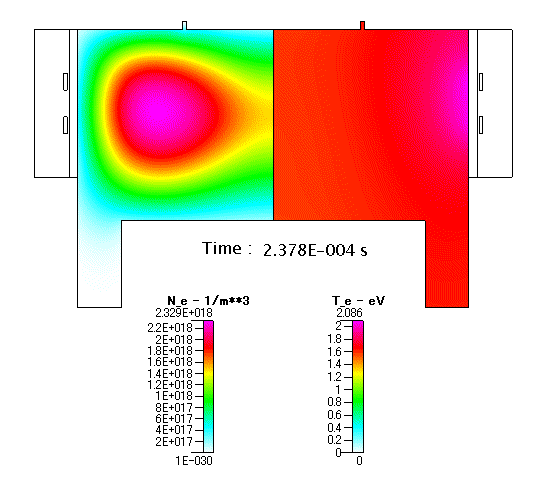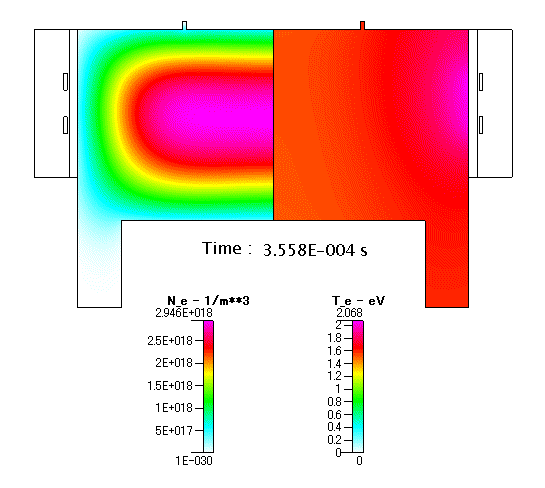
Fig. 12 放電開始以降の Ne 及び Te の分布(アニメーション)
予想されるように,始めはアンテナに近い領域で Ne の高いリング上のプラズマが生成されます.そして,時間が経過するに従って,定常状態の結果に示されるように,チャンバーの中央へと高密度の領域がシュリンクして行く様子が分かります.
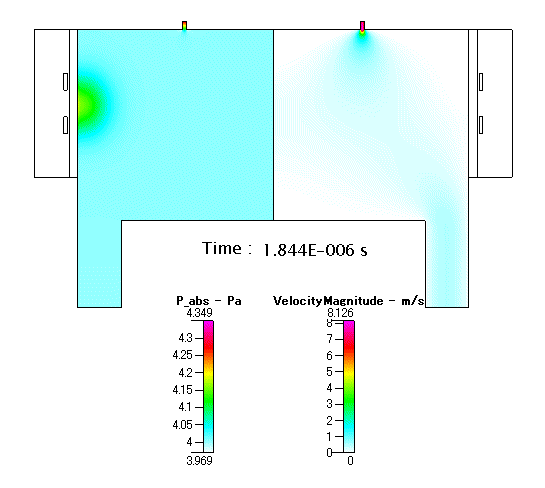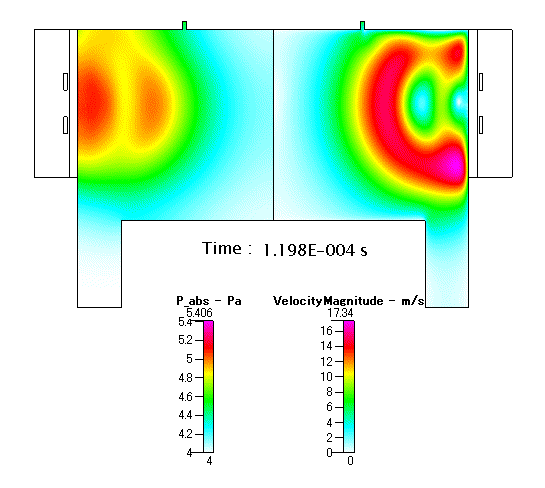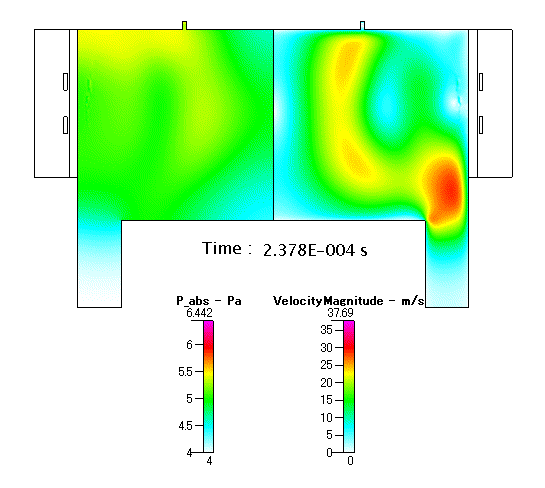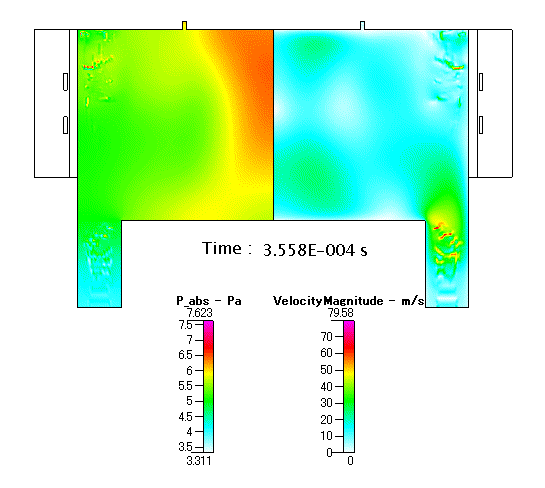
Fig. 13 放電開始以降の 圧力 及び 流速 の分布(アニメーション)
プラズマの成長とシュリンクに伴い,内部の圧力や流速は,ダイナミックに変化することがシミュレーションの結果から推測されます.圧力は,始めにアンテナ近傍で高くなり,チャンバー内へと伝搬して行きます.流速も,アンテナ近傍で高くなり,同様にチャンバー内へと伝搬して行きます.流速の最大値は,最大で 50m/s 以上という非常に速い値に到達し,内部で跳ね返るように最終的には outlet に向ってガスが向うと考えられます.
☆
最後に,1周期の中での変化について,渦電流・ベクトルポテンシャル(Az)の結果を以下に示します.Fig. 4 の渦電流( J_eddy )は,定常解析の結果ですが,実際には,RFコイルの電流が変化するにつれて,渦電流も変化します.
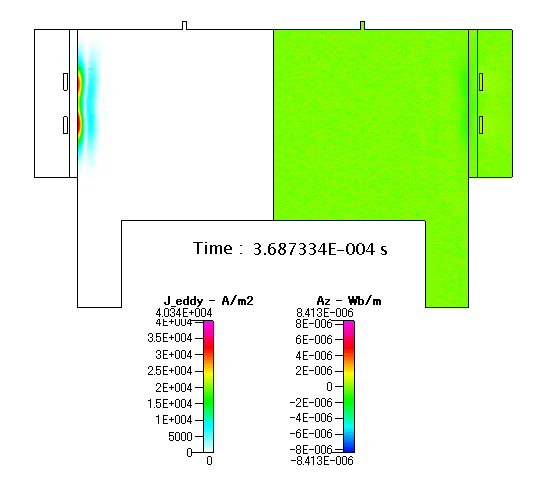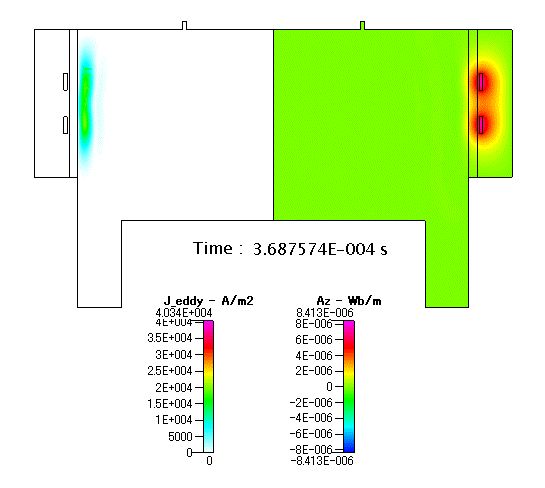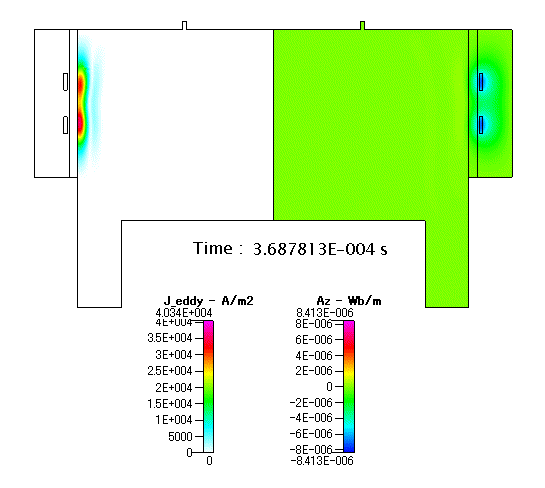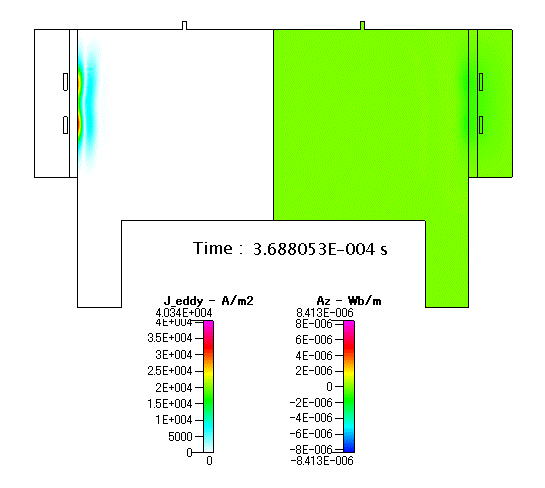
Fig. 14 渦電流( J_eddy )及び ベクトルポテンシャル(Az)の分布(アニメーション)
☆
本計算では,用いた grid が計算精度を保つのに十分ではなかった為,計算の最後の方では,十分収束した結果になりませんでしたが,放電直後にどのような現象が起きているかを,シミュレーションを利用して理解することができます.また,これらの結果は,過去の経験を裏付けると共に,着火という難易度の高い問題に取り組む第一段階と考えられます.
☆
本計算は,現在 grid を修正し,ベターな結果が得られるように再計算中です(詳しくは,11/18-19に予定されている ESI Users' Forum Japan 2010 でご紹介する予定でしたが,講演数超過により,別の機会とさせて頂きます).また,CFD-ACE+ で利用できる CCP mode による解析を行うことにより,より現実的な解析も可能で,現在,その計算にも取り組んでいます.
この CCP mode によるシミュレーション手法を確立することで,放電開始時の異常放電がどういう箇所で起き易いか,という問題に対し,その対策を考えるヒントを与えると期待されます.
更新履歴:
Aug. 15 2010 upload
Sep. 21 2010 1周期内の渦電流・Az の結果を追加
☆
back to home > products > CFD-ACE+
© 2008- ATHENASYS Co., Ltd. All Rights Reserved.
