逐次反応で生じる連立微分方程式の計算例（ mathematica ）

逐次反応で生じる連立微分方程式の計算例 ( stepwise reation ）

反応が一次で表され，A -> B，及び，B -> C のように変化するのは，実際の反応でも現れることのある例の一つです．

反応を考慮した流体シミュレーションを実際に行って検証することも勿論可能ですが，例えば，A が原料ガスの場合，原料の供給量が十分か，或は，その利用効率は，といった概略を知りたいような場合に，mathematica で微分方程式を連立させて解き，見通しを立てる，といったことが可能です．

species A，B，C の濃度を，cA，cB，cC とすると，釣り合いの式は，以下のように表されます．

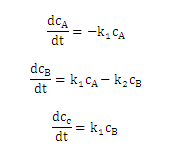
連立微分方程式

ここで，k₁ 及び k₂ は，A -> B，及び，B -> C へ進む際の反応レートとします．mathematica では，例えば，以下のように記述することが出来ます．なお，便宜的に，k₁ = 10，k₂ = 20，としています．

mathematica の input

mathematica での input の例

時間ゼロの時点では，cA = 10，cB = cC = 0 を仮定します．

計算された各濃度は，以下のようなグラフで示されます．

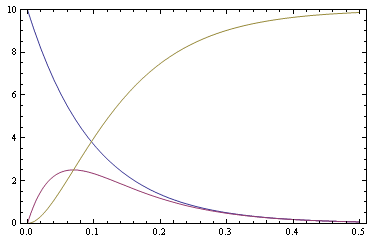
各 species の時間に対する濃度

各species の時間に対する濃度（青->cA，赤->cB，黄色->cC）

cA（図中の青線）は時間とともに単調に減少しますが，cB（図中の赤線）は，ピークを持つ様子が示されています．最終生成物の cC（図中の黄色線）は，単調に増加してある程度の時間が経過すると飽和します．

このように，連立微分方程式を解いてグラフ化するのに数行で済む点は，mathematica の良さの一つと言えます．

☆