Manipulate を使った管内の液中高さ（メニスカス）の計算例

Manipulate を使った管内の液柱高さ（メニスカス）の計算例

理論的な解が分かっているような場合，ソフトウェアの機能を確認するために，その式を用いて実際に計算を行ってみることがあります．

管内の液柱の高さは，一般に，表面張力によって元の液面の高さよりも異なることが知られています．ここでは，理論的な計算から予測される高さを mathematica で計算し，また，CFD-ACE+ を用いて実際に計算を行い，結果を比較してみました．

計算条件は，以下の通りです．

始めに，CFD-ACE+ を用いた流体シミュレーションの結果を示します．

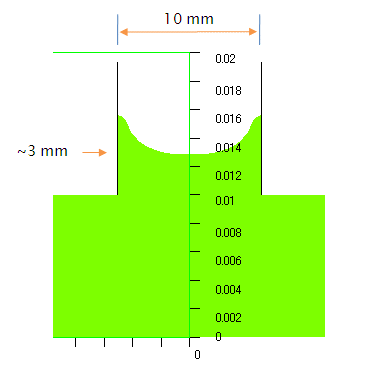
メニスカス（ meniscus ）を CFD-ACE+ を用いて計算した結果

Fig. 1　CFD-ACE+ の Free Surface (VOF) を用いて計算した結果

次に，Mathematica の Manipulate を用いて，表面張力（ sigma ），接触角（ theta ），液体の密度（ rhoL ），気体の密度（ rhoG ）を可変の変数とし，横軸に管径 [m]，縦軸に，境界面の高さ [m]，を算出してみました．

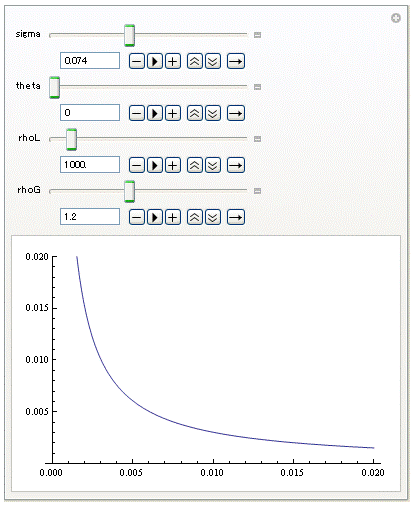
mathematica の Manipulate 機能を用い，円管内の液柱高さを計算・表示した結果

Fig. 2　管内の液柱の高さを Mathematica 計算・表示した例

実際に，今回の固定値で計算される境界面の高さは 3.0 mm で，CFD-ACE+ の計算結果が妥当なことも確かめられました．また，管径が小さくなると，液柱の高さが急激に上昇することも分かります．

☆

U を代表速度，L を代表長さ，ρを密度，表面張力をσ，とすると，慣性力と表面張力の比は，

ρU²L²/σL = ρU²L/σ= We²

となります．ここで，We はウェーバー数（ Weber number ）として知られる無次元数になります．We数が等しければ，表面張力が重要な流れが力学的な相似則を満たす条件となります．インクジェットプリンタ等の液滴生成をシミュレーションする場合には，この We数に着目した解析が重要となります．

☆

参考文献：

　例題で分かる基礎・演習　流体力学（ ISBN4-320-08148-X ）

☆