( Estimation of pre-exponential factor and activation energy with experimental data )
反応モデルがアレニウス型(Arrhenius equation)で表され,実験的に得られたアレニウスプロットがある場合には,その反応速度式の頻度因子( pre-exponential factor)と見かけの活性化エネルギー( activation energy )を見積もることができます.ここで「見かけ」と呼ぶのは,実験結果で得られる反応の多くは素反応ではなく,ある律速過程に対して適用できる場合が多いため,出来るだけ誤解を避ける意味でつけていますが,以下は,単に活性化エネルギーとして話を進めます.
☆
アレニウス型の式(外部サイト:wiki)は,反応速度を表現するために頻度因子と活性化エネルギーが求まると,温度に依存したアレニウス型の反応速度を求める式となります.アレニウスプロットは,横軸に温度の逆数(通常,逆数をとって1000倍します)をとり,縦軸に反応速度の自然対数をとった値を用います.手元の演習書(*1)に例題(アセトアルデヒドの分解反応)がありますので,その例を取り上げてみます.
| T(K) | 700 | 730 | 760 | 790 | 810 | 840 | 910 | 1000 |
| k | 0.011 | 0.035 | 0.105 | 0.343 | 0.789 | 2.17 | 20.0 | 145 |
今回は,フィッティングに mathematica 6 を用いました.始めに,自然対数をとらず,そのままの値をプロットしてみます.
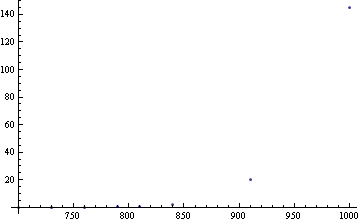
Fig. 1 温度(横軸)に対する反応速度(縦軸)のプロット
この結果に対し,フィッティングを行った結果とカーブが以下のようになります.
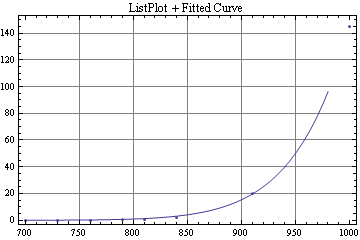
Fig. 2 温度(横軸)に対する反応速度(縦軸)のプロットデータとフィットさせた曲線
フィッティングの結果から,頻度因子:8.83171E10,活性化エネルギー:168170,がそれぞれ得られました.ちなみに,演習書の解としては,頻度因子:5.06E11,活性化エネルギー:183490 となっており,かなり差のあることが分かります.
次に,温度に対して逆数をとり,1000倍した値を横軸にとったグラフと,縦軸に反応速度の ln(自然対数)をとった値をプロットしてみます.
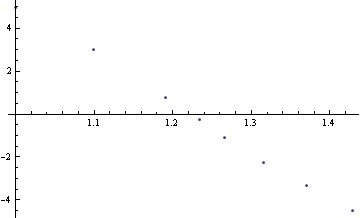
Fig. 3 1000/T(横軸)に対する ln(k)(縦軸)のプロットデータ
この結果に対し,フィッティングを行った結果の直線が以下のようになります.
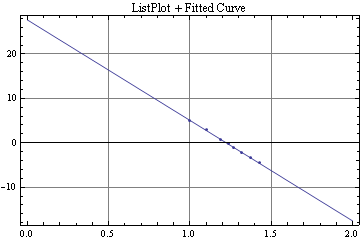
Fig. 4 1000/T(横軸)に対する ln(k)(縦軸)のプロットデータとフィットさせた直線
フィッティングの結果から,頻度因子:1.07906E12,活性化エネルギー:188318,がそれぞれ得られました.活性化エネルギーの値は,約3%ずれていますが,演習書の値とほぼ同じ結果が得られました.
頻度因子の値は,ほぼ倍,異なっていますが,先のフィッティングの結果よりはずっと演習書の結果に近いことが確かめられました.頻度因子の値は,グラフの y切片から計算するため,活性化エネルギーの見積りが僅かに違うだけでも,Exp(y切片)として得られる結果に大きく影響してしまうことが分かります.言い換えると,実験結果から見積もられる頻度因子に対しては,数倍程度は誤差は予め覚悟する必要がある,とも言えそうです.
☆
Fig. 3 及び Fig. 4 の作成,及び,頻度因子と活性化エネルギーの計算には,以下の input file を用いました.

この例では,予め対数をとって整理された text file を読み込み,FindFit と呼ぶ関数を用いてフィッティングを行っています.そして,result という配列の中に取り込んだ結果から,頻度因子と活性化エネルギーを計算して算出しています.
参考文献:
1)REA's Problem Solvers : Physical Chemistry [ISBN : 0-87891-532-X]
☆
© 2008- ATHENASYS Co., Ltd. All Rights Reserved.
