Investigation of the temperature profile in a hot-wall SiC chemical vapor deposition reactor
O. Danielsson et. al.
Journal of Crystal Growth 235(2002) 352-364
< Update : Feb. 9 2009 >
温度が比較的高い熱CVD装置(以下,単にCVD装置と略す)の場合,成膜や結晶成長を行う温度を実現する方法として,しばしば誘導加熱が利用されます.誘導加熱は,交流を印可するコイルを用いますが,コイルの形状,巻数,位置,周波数等の色々なパラメータがあり,また,一つだけでなく,複数のコイルを同時に使用される場合もあります.
温度分布の最適化は,CVD装置の設計では最も重要な点の一つで,設計が良くないと,他のパラメータ(ガス流量や圧力,等)をどんなに最適化しても,期待している成膜分布や膜質分布が得られない,といった問題が生じます.そのため,新しく装置を設計したり,既存の装置を改良しようとする場合,事前に熱解析を行う必要があります.
今回取り上げる論文では,実験装置との比較を行いながら計算モデルの妥当性を評価・確認しつつ,理想的な温度分布を実現するために行った様々な検討内容が紹介されています.装置形状はシンプルですが,他の複雑な装置を検討する前に,知っておいて損のないことが述べられていると思われます.
論文では,シミュレーションに CFD-ACE+ が利用されていますので,当社で同様の計算モデルを準備・作成しました.以下では,当社での計算例を示します.
☆
実際の実験装置を詳細にモデル化するには3次元の解析モデルが必要ですが,実験装置の形状はシンプルで,2次元軸対称とみなせます.そのため,3次元の解析を行う前のほとんどの検討は,2次元軸対称モデルで行われています.計算モデルの概略を以下に示します.
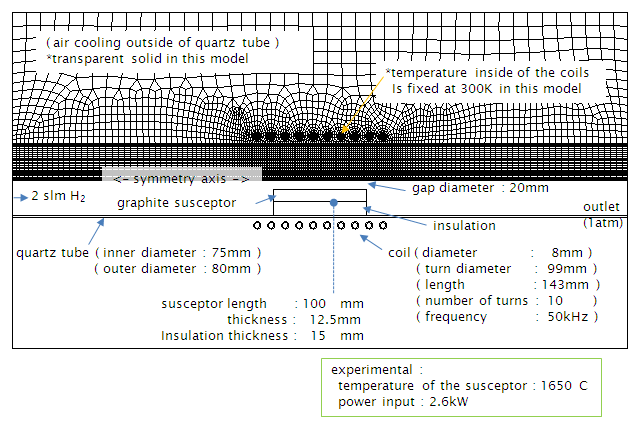
Fig. 1 計算モデルの概略
記述している寸法については,論文の中で説明されています.標準条件として,圧力:1000mbar,H2流量:2slm(以下の結果は流量 0.5slm の計算例でした.お詫びして訂正させて頂きます [ Feb. 9 2009 ] ),サセプター(suceptor)の中央における温度:1650℃ となっています.
シミュレーションでは熱輻射( Decreate Ordinate Method )を考慮し,石英については Non-Gray として波長域を2つ(0〜3.5μm:透明,3.5μm〜∞:不透明)に分けました.電力については,2.6kW と論文に記載されていますが,これに近い電力の際に,サセプター温度を1650℃程度となるようにするには,石英管( quartz tube )が空冷によって結構冷やされていることを考慮する必要があるようです.
論文では,空冷に関する詳細は述べられていないため,本シミュレーションでは,石英管周囲の空気流れを流体としては計算せず,熱伝導率が空気よりも高い透明な固体としてモデル化しました.今回用いた熱伝導率は,0.15[W/m-K] という値を用いています.空気の流れを実際に乱流モデルで計算した,得られた熱伝導率を評価すると,石英管近傍では 0.15 より高い値となっており,平均的な値としては,ある程度妥当な範囲に入っていると考えられます.なお,石英管よりも外側に位置する計算領域の最外周においても,熱伝達係数・輻射率を仮定し,熱の逃げを考慮しました.
以下に,サセプター近傍を拡大した図を示します.
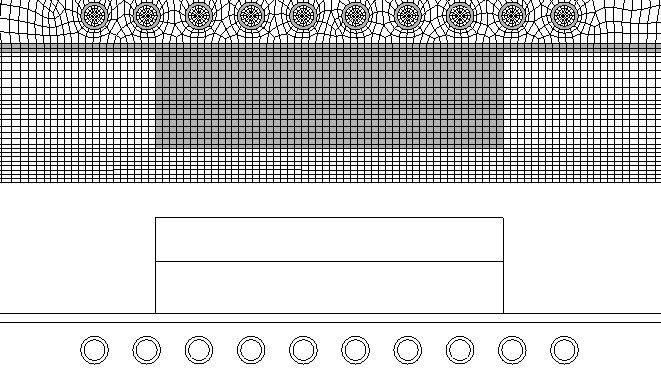
Fig. 2 計算モデルの概略(サセプター近傍)
コイル内部は,水冷されている場合が多いため,本シミュレーションでは 300K 一定としました.また,輻射が支配的な比較的温度の高い条件となっており,各部材間の熱抵抗は無視しました.各部材の熱伝導率や電気抵抗率等は,温度に対する多項式の近似式が論文に記載されており,同じ設定を行いました.
電力が消費される部材(有限の電気抵抗率を与えた部材)は,サセプターと断熱材( insulation )のみですが,断熱材の電気抵抗率は比較的高く,吸収される電力の大部分がサセプターに集中します.
以下,サセプター温度がほぼ1650℃となる条件(コイル電流:143.2A)の計算結果を示します.
■ 圧力,及び,流速分布
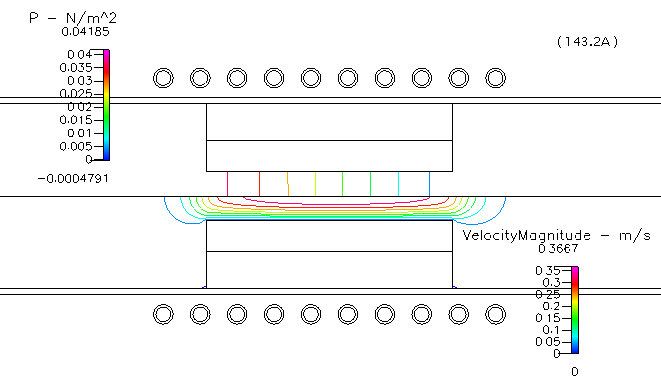
Fig. 3 圧力,及び,流速分布
流体部は,compressible flow( ideal gas )として計算しましたが,出口( 1atm )に対する圧力差は非常に小さいことが分かります(論文では,imcompressible として取り扱われています).また,サセプターの部分で流れに対する断面積が小さくなりますが,以下の図5 からも分かる通り,2slm の条件では,サセプターの温度分布に与える影響が比較的小さく抑えられています.なお,流量を 8slm に増やすと,サセプターの温度分布はガス流速の影響をかなり強く受けている様子が論文では示されています(ここでは,割愛します).
■ ベクトルポテンシャル( Az_i,Az_i )
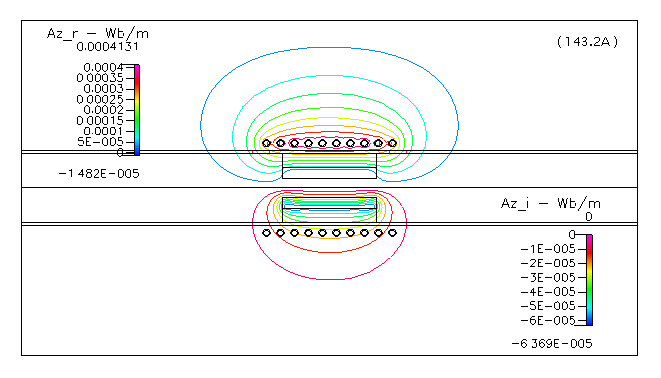
Fig. 4 Magnetic Vector Potential Az_i 及び Az_i
ジュール加熱を計算するためにマクスウェル方程式を解きますが,ここではベクトルポテンシャルを計算しています.z は,2軸対称モデルでは周方向になります.コイルの部分で Az_r(実数部)が高く,サセプターの部分で Az_i(虚数部)の絶対値が大きくなっていることを示しています.
■ 温度分布,及び,吸収電力
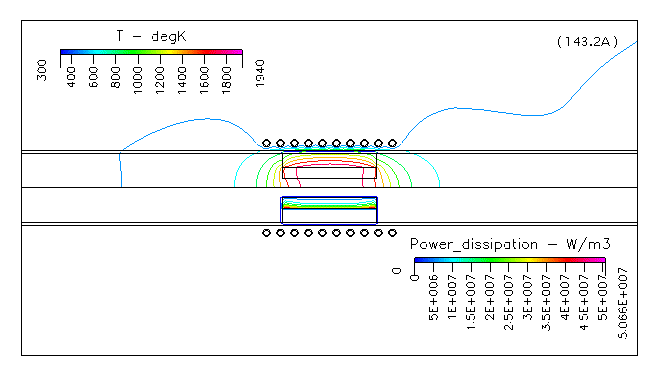
Fig. 5 温度分布,及び,サセプター内の吸収電力(コイルの周波数:30kHz)
サセプターの中央で最も温度が高く,端部では熱輻射によって温度が下がっていることを示しています.以下に,サセプター近傍を拡大して示します.
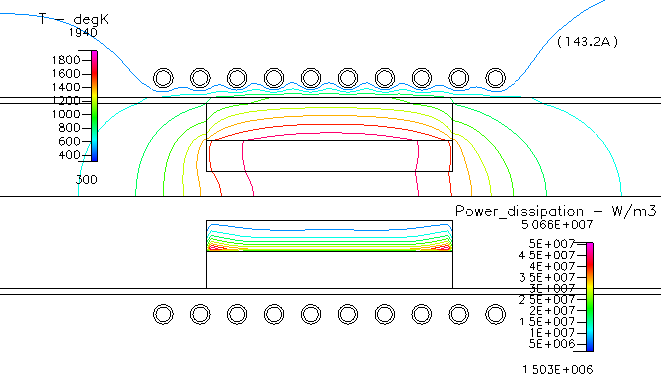
Fig. 6 温度分布,及び,サセプター内の吸収電力(サセプター近傍)
電力の吸収が最も大きいのは,サセプター内の断熱材に隣接する付近で,端部に近い部分に集中している様子が分かりますが,10ターンのコイルに対して均等な電流を仮定しているこの計算例では,サセプター内にかなり大きな温度分布が生じることを示しています.論文では,異なる電力による温度分布も示されていますが,いずれの場合もサセプター内に大きな温度差が生じています.
周波数が高くなるにつれて,表皮効果の影響が無視出来なくなることが知られていますが,その影響を比較するために,電流値はそのままで,30kz・70kHz についても計算してみました(論文では,20kHz 及び 70kHz の例が示されています).
■ コイル周波数依存性(コイルの周波数 30kHz/70kHz の場合)
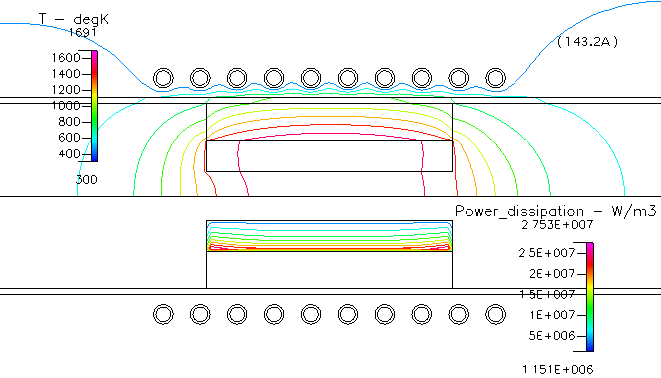
Fig. 7 温度分布,及び,サセプター内の吸収電力(コイルの周波数:30kHz)
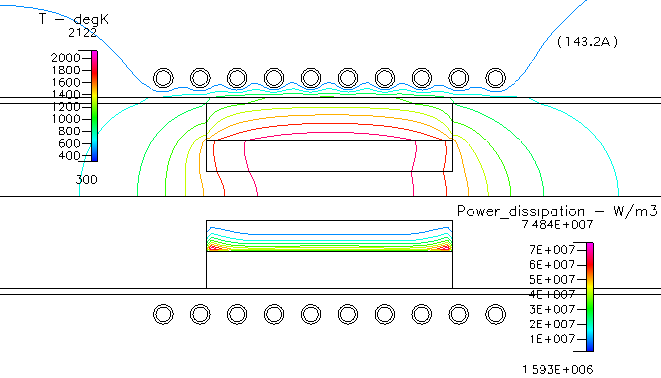
Fig. 8 温度分布,及び,サセプター内の吸収電力(コイルの周波数:70kHz)
Fig. 9 異なる周波数に対するサセプターの温度分布
電力も異なりますので単純な比較は出来ませんが,周波数が高いと電力の吸収がより狭い領域に限定され,結果的に温度差を大きくします.
論文では,この他にも,サセプターの厚さ,コイルの位置や形状,ターン数,断熱材の追加,等についても議論されており,また,非定常の計算も行って,温度上昇カーブに関し,実験結果に近い傾向が得られることを確かめています.最後に,最適化した条件を元に3次元の計算モデルでシミュレーションを行い,サセプター内の広い領域で温度の均一性を向上させた結果が示されています.
☆
ここでは,計算条件の詳細も分からないため,全ての追試は行いませんが,10ターンのコイルを3つに分割し,温度分布を最適化出来るか検討してみましたので,参考までにご紹介します.
まず,サセプターの端部を効率的に加熱することを前提に,周波数は高い70kHz としました.10ターンあるコイルを,左から3ターン,中央付近の2ターン,及び,向って右側から3ターンの3つの領域に分け,残り2ターンの部分はないものとして考えます(計算モデルでは,端から数えて4番目と7番目の電流値をゼロとしました).そのモデルにおいて,両側の3ターンの部分には248A,中央の2ターンの部分には66Aを流した場合の結果を,元の 50kHz の条件と比較したものが,以下になります.
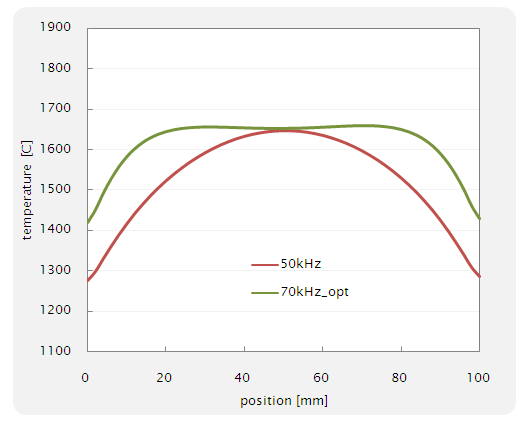
Fig. 10 周波数:70kHz で最適化されたサセプターの温度分布
この計算条件では,サセプター上 20〜80mm の範囲で,温度の不均一性を非常に小さくできることが分かりました.このように,シミュレーションをうまく活用することで,事前に最適な条件を検討することが可能となります.
☆
一般に,シンプルな2次元,或は2次元軸対称のモデルで実験結果との比較を行い,物性値や境界条件等の妥当性を吟味・確認した上で,3次元モデルへと移行するのが効率的です.本論文でも,可能な検討を事前に2次元モデルで行い,最後に3次元モデルでの確認を行う,という手順を踏んでいます.
反応を考慮する計算は,より計算時間が掛かるだけでなく,考慮するパラメータの数が非常に多くなります.そのため,実験結果との不一致の原因を検討する際,その問題が反応モデルに起因するのか,或は熱解析モデルに起因するのかを見極めるのは,一般に困難になります.従って,反応を考慮する前に必ず熱解析モデルを準備・検討し,その妥当性を十分評価しておくことが重要となります(Danielsson氏自身,この論文を出された後に,詳細な反応を考慮した論文を出されています).
☆
Feb. 9 2009 : additional comment on the smaller flow rate of H2 in the calculation
Feb. 3 2009 : up
back to home > learn_from_others
© 2008 ATHENASYS Co., Ltd. All Rights Reserved.
